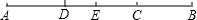(本小题满分7分)
解:(1)AF=CD.
(2)变换后的菱形BDEF如图,结论AF=CD仍然成立.

理由:在等边△ABC中,AB=BC,
在菱形BDEF中,BF=BD.
∵DF=DB,∴DF=DB=BF.
∴∠FBD=∠ABC=60°.
∴∠FBD-∠1=∠ABC-∠1.
即∠2=∠3.
∴△ABF≌△CBD.
∴AF=CD.
(3)不变化;60°.
设CD与AF交于点O,与AB交于点G,
由(2)知:∠BAF=∠BCD,
又∠AGO=∠CGB,
∴∠AOC=∠ABC=60°.
即AF与CD所夹锐角始终为60°.
分析:(1)根据△AFB≌△CDB可以得到两线段相等;
(2)图形变化后一般情况下结论不变,在此基础上进一步证明两个三角形全等即可得到正确的结论;
(3)设CD与AF交于点O,与AB交于点G,证得∠AOC=∠ABC=60°即可.
点评:本题考查了旋转的性质,解题的关键是正确的利用旋转不变量,从而为证明全等提供必要的条件.

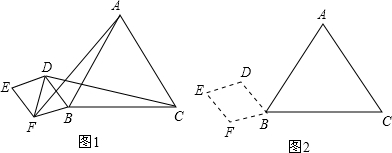



 已知,如图,DC∥AB,且DC=
已知,如图,DC∥AB,且DC=