已知:矩形ABCD在平面直角坐标系中,顶点A、B、D的坐标分别为A(0,0),B(m,0),D(0,4),其中m≠0.
(1)写出顶点C的坐标和矩形ABCD的中心P点的坐标(用含m的代数式表示);
(2)若一次函数y=kx-1的图象J把矩形ABCD分成面积相等的两部分,求此一次函数的解析式(用含m的代数式表示);
(3)在(2)的前提下,l又与半径为1的⊙M相切,且点M(0,1),求此时矩形ABCD的中心P点的坐标.
分析:(1)由图象可以写出C点的坐标,P为矩形的中心,由中点坐标公式可以写出P点坐标.(2)设出函数解析式,因为一次函数y=kx-1的图象J把矩形ABCD分成面积相等的两部分,故直线经过中心,把中心坐标代入,解出函数解析式.(3)在(2)的条件下,又增加了一条件,求出m.
解答: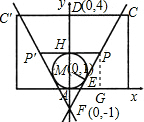
解:(1)C点坐标为(m,4)
P点坐标为(
,2).
(2)∵直线L把矩形ABCD分成面积相等的两部分.
∴L必过中心点P(
,2),
∴4=km-2,
∵m≠0,∴k=
,
∴y=
x-1.
(3)设直线l与y轴相交于点F,
∴F点坐标为(0,-1),
∵⊙m的半径为1,
∴sin∠EFD=
=
,
∴∠EFD=30°.
过P作PH⊥y轴于H
∴
=tan∠EFD=tan30°=
,
∴PH=
FH=
,
∴
||=,
∴p点坐标(±
,2).
点评:本题主要考查一次函数的应用,熟悉一次函数的解析式的求解.

 解:(1)C点坐标为(m,4)
解:(1)C点坐标为(m,4)

 培优口算题卡系列答案
培优口算题卡系列答案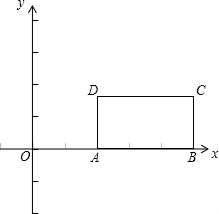 已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=
已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=