
分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边16既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即16是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为x,
(1)若16是直角边,则第三边x是斜边,由勾股定理得:
122+162=x2,所以x=20;
(2)若16是斜边,则第三边x为直角边,由勾股定理得:
122+x2=162,所以x=4$\sqrt{7}$;
所以三角形的第三边是20或4$\sqrt{7}$.
故答案为:20或4$\sqrt{7}$.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.


科目:初中数学 来源: 题型:填空题
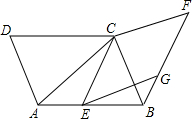 如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号).
如图,点E是平行四边形ABCD的边AB上的任意一点(不包含端点A,B),分别连接AC,CE,以CE为边作菱形ECFG,再连接BG,已知AB=AC,∠CEG=∠CAB,则下列结论①EG⊥BC,②∠EGB=∠F,③∠CBG=∠CAB,④∠GEB=∠ACE中,一定成立的有②③④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A、B、C、D四点如图所示,请按如图的要求作图
已知A、B、C、D四点如图所示,请按如图的要求作图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com