
【题目】如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.

(1)求点O到BD的距离及∠OBD的度数;
(2)若DE=2BE,求![]() 的值和CD的长.
的值和CD的长.
【答案】(1)O到BD的距离为1;![]() ;(2)
;(2)![]() ;
;![]()
【解析】
试题(1)作OF⊥BD于点F,连接OD,根据圆周角定理可得出∠DOB=120°,再由OB=OD=![]() AC=2,可得出∠OBD的度数,也可得出OF的长度;
AC=2,可得出∠OBD的度数,也可得出OF的长度;
(2)设BE=2x,则可表示出DF、EF的长度,从而可解出x的值,在RT△OEF中,利用三角函数值的知识可求出∠OED的度数,也可得出cos∠OED的值,判断出DO⊥AC,然后利用等腰直角三角形的性质可得出CD的长度.
(1)作OF⊥BD于点F,连接OD,
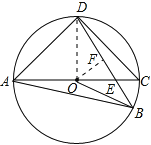
∵∠BAD=60°,
∴∠BOD=2∠BAD=120°,
又∵OB=OD,
∴∠OBD=30°,
∵AC为⊙O的直径,AC=4,
∴OB=OD=2.
在Rt△BOF中,∵∠OFB=90°,OB=2,∠OBF=30°,
∴OF=OBsin∠OBF=2sin30°=1,
即点O到BD的距离等于1;
(2)∵OB=OD,OF⊥BD于点F,
∴BF=DF.
由DE=2BE,设BE=2x,则DE=4x,BD=6x,EF=x,BF=3x.
∵BF=OBcos30°![]()
∴![]() ,
,![]()
在Rt△OEF中,∠OFE=90°,∵tan∠OED=![]()
∴∠OED=60°,cos∠OED=![]() ,
,
∴∠BOE=∠OED-∠OBD=30°,
∴∠DOC=∠DOB-∠BOE=90°,
∴∠C=45°
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】对![]() ,
,![]() 定义一种新的运算
定义一种新的运算![]() ,规定:
,规定:![]()
 (其中
(其中![]() ).已知
).已知![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若关于正数![]() 的不等式组
的不等式组 恰好有2个整数解,求
恰好有2个整数解,求![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 时,满足条件的
时,满足条件的![]() ,
,![]() 的关系.
的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )

A. 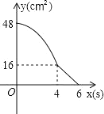 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
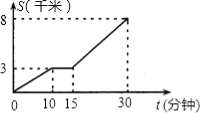
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com