
 øöµ„Ī»µÄĖŁ¶ČŅĘ¶Æ£¬Čē¹ūP£¬Q·Ö±š“ÓD£¬BĶ¬Ź±³ö·¢£®
øöµ„Ī»µÄĖŁ¶ČŅĘ¶Æ£¬Čē¹ūP£¬Q·Ö±š“ÓD£¬BĶ¬Ź±³ö·¢£®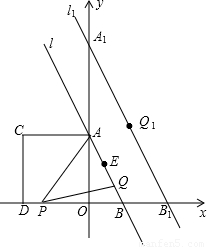
 t£¬ŌŚRt”÷AOBÖŠ£¬Ēó³öABµÄ³¤¶Č£¬×÷QF”ĶOBÓŚF£¬½įŗĻĢāøÉĢõ¼ž£¬Ö¤Ć÷”÷QFB”×”÷AOB£¬ÓĆt±ķŹ¾³öQF£¬S=S”÷PBA-S”÷PBQ£¬½ų¶ųĒó³öSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµ£»
t£¬ŌŚRt”÷AOBÖŠ£¬Ēó³öABµÄ³¤¶Č£¬×÷QF”ĶOBÓŚF£¬½įŗĻĢāøÉĢõ¼ž£¬Ö¤Ć÷”÷QFB”×”÷AOB£¬ÓĆt±ķŹ¾³öQF£¬S=S”÷PBA-S”÷PBQ£¬½ų¶ųĒó³öSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµ£»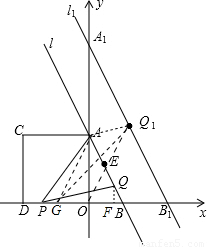 ½ā£ŗ£Ø1£©”ßÖ±Ļßl£ŗy=-2x+4½»yÖįÓŚAµć£¬½»xÖįÓŚBµć£¬
½ā£ŗ£Ø1£©”ßÖ±Ļßl£ŗy=-2x+4½»yÖįÓŚAµć£¬½»xÖįÓŚBµć£¬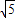 t£¬
t£¬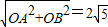 £¬
£¬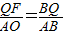 £¬
£¬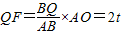 £¬
£¬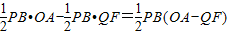 £¬
£¬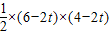 £¬
£¬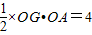 £¬
£¬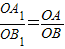 £¬
£¬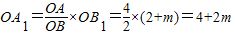 £¬
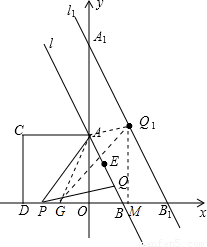
£¬
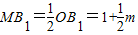 £¬
£¬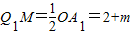 £¬
£¬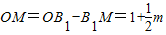 £¬
£¬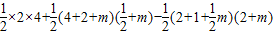


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 13”¢ČēĶ¼£¬Ö±Ļßa”¢b¶¼ÓėÖ±ĻßcĻą½»£¬øų³öĻĀĮŠĢõ¼ž£ŗ£Ø1£©”Ļl=”Ļ2£»£Ø2£©”Ļ3=”Ļ6£»£Ø3£©”Ļ4+”Ļ7=180”ć£»£Ø4£©”Ļ5+”Ļ8=180”ć£¬ĘäÖŠÄÜÅŠ¶Ļa”ĪbµÄŹĒ£Ø””””£©
13”¢ČēĶ¼£¬Ö±Ļßa”¢b¶¼ÓėÖ±ĻßcĻą½»£¬øų³öĻĀĮŠĢõ¼ž£ŗ£Ø1£©”Ļl=”Ļ2£»£Ø2£©”Ļ3=”Ļ6£»£Ø3£©”Ļ4+”Ļ7=180”ć£»£Ø4£©”Ļ5+”Ļ8=180”ć£¬ĘäÖŠÄÜÅŠ¶Ļa”ĪbµÄŹĒ£Ø””””£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 4”¢ČēĶ¼£¬Ö±ĻßAB”¢CDĻą½»ÓŚµćE£¬EF”ĶABÓŚE£¬Čō”ĻCEF=59”ć£¬Ōņ”ĻAEDµÄ¶ČŹżĪŖ£Ø””””£©
4”¢ČēĶ¼£¬Ö±ĻßAB”¢CDĻą½»ÓŚµćE£¬EF”ĶABÓŚE£¬Čō”ĻCEF=59”ć£¬Ōņ”ĻAEDµÄ¶ČŹżĪŖ£Ø””””£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ČēĶ¼£¬Ö±Ļßy=6-x½»xÖį”¢yÖįÓŚA”¢BĮ½µć£¬PŹĒ·“±ČĄżŗÆŹży=
ČēĶ¼£¬Ö±Ļßy=6-x½»xÖį”¢yÖįÓŚA”¢BĮ½µć£¬PŹĒ·“±ČĄżŗÆŹży=| 4 |
| x |
| AӢ8 | ||
| BӢ6 | ||
| CӢ4 | ||
DӢ6
|
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 17”¢ČēĶ¼£¬Ö±Ļßa”Īc£¬b”Īc£¬Ö±ĻßdÓėÖ±Ļßa”¢b”¢cĻą½»£¬ŅŃÖŖ”Ļ1=60”ć£¬Ēó”Ļ2”¢”Ļ3µÄ¶ČŹż£ØæÉŌŚĶ¼ÖŠÓĆŹż×Ö±ķŹ¾½Ē£©£®
17”¢ČēĶ¼£¬Ö±Ļßa”Īc£¬b”Īc£¬Ö±ĻßdÓėÖ±Ļßa”¢b”¢cĻą½»£¬ŅŃÖŖ”Ļ1=60”ć£¬Ēó”Ļ2”¢”Ļ3µÄ¶ČŹż£ØæÉŌŚĶ¼ÖŠÓĆŹż×Ö±ķŹ¾½Ē£©£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com