
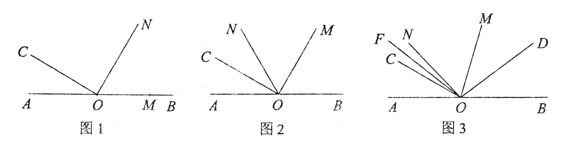
【题目】如图1, 点![]() 在直线
在直线![]() 上,
上,![]() ,将.
,将.![]() 绕着点
绕着点![]() 以
以![]() 的速度逆时针旋转,设旋转时间为
的速度逆时针旋转,设旋转时间为![]() .
.
(1)如图2,当![]() 平分
平分![]() 时,
时,![]() ______
______![]() ; 图中
; 图中![]() 的补角有: ______;
的补角有: ______;
(2)如图3,当![]() 时,
时,![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(3)在![]() 绕着点
绕着点![]() 逆时针旋转的过程中,当
逆时针旋转的过程中,当![]() ______
______![]() 时,
时,![]() .
.
【答案】(1)![]() ; 图中
; 图中![]() 的补角有:
的补角有: ![]() 和
和![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]()
【解析】
(1)根据角平分线的性质求出∠AON的度数,进而求出∠BON和∠BOM的度数,再根据“时间=路程÷速度”,即可得出答案;根据补角的定义即可得出答案;
(2)先设出∠BOM和∠CON的度数,再根据角平分线的定义求出∠NOF和∠DOM的度数,即可得出答案;
(3)分情况进行讨论,①当ON位于直线AB上方,OM位于∠BOC中时;②当ON位于直线AB下方,OM位于∠AOC中时;③OM和ON均位于直线AB下方时;④当ON位于直线AB上方,OM位于直线AB下方时;分别求出每种情况下∠AON和∠COM的度数,再令∠AON=∠COM,解方程即可得出答案.
解:(1)当OC平分∠AON时,∠AON=2∠AOC=60°
∴∠BON=120°
又∠MON=60°
∴∠BOM=∠BON-∠MON=60°
∴t=60÷10=6(s);
图中![]() 的补角有:
的补角有:![]() 和
和![]() ;
;
(2) ∵运动时间为![]() 秒,运动速度为
秒,运动速度为![]() ,则
,则
![]()
又∵![]() 平分
平分![]() ,
,![]() 平分
平分![]()
∴![]() ,
,
![]()
∴![]()
∴当![]() 时,
时,![]() 的度数为
的度数为![]()
(3)①当ON位于直线AB上方,OM位于∠BOC中时
∠AON=(120-10t)°,∠COM=(150-10t)°
又∠AON=∠COM,即(120-10t)°=(150-10t)°,无解;
②当ON位于直线AB下方,OM位于∠AOC中时
∠COM=(150-10t)°,∠AON=(10t-120)°
又∠AON=∠COM,即(150-10t)°=(10t-120)°,解得t=13.5;
③OM和ON均位于直线AB下方时
∠COM=(10t-150)°,∠AON=(10t-120)°
又∠AON=∠COM,即(10t-150)°=(10t-120)°,无解;
④当ON位于直线AB上方,OM位于直线AB下方时
∠COM=(10t-150)°,∠AON=(480-10t)°
又∠AON=∠COM,即(10t-150)°=(480-10t)°,解得t=31.5;
∴当![]() 或
或![]() 时,
时,![]()


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
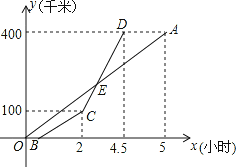
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售量 | 销售收入 | |
A型号 | B型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
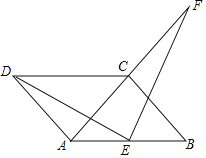
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() , 将一直角的直角项点放在点
, 将一直角的直角项点放在点![]() 处,即
处,即![]() 反向延长射线
反向延长射线![]() ,得到射线
,得到射线![]() .
.
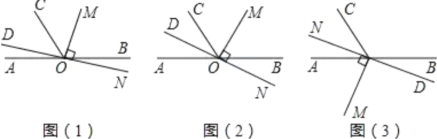
(1)当![]() 的位置如图(1)所示时,使
的位置如图(1)所示时,使![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
(2)当![]() 的位置如图(2)所示时,使一边
的位置如图(2)所示时,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,
,
问:射线![]() 的反向延长线
的反向延长线![]() 是否平分
是否平分![]() 请说明理由:注意:不能用问题
请说明理由:注意:不能用问题![]() 中的条件
中的条件
(3)当![]() 的位置如图
的位置如图![]() 所示时,射线
所示时,射线![]() 在
在![]() 的内部,若
的内部,若![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,不需要证明,直接写出结论.
之间的数量关系,不需要证明,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
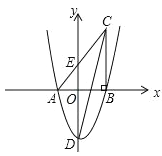
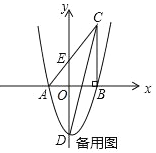
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
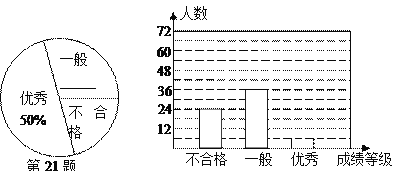
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
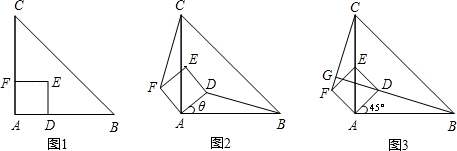
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商场销售一种茶具和茶碗,茶具每套定价2000元,茶碗每只定价200元,“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一套茶具送一只茶碗;方案二,茶具和茶碗按定价的九五折付款,现在某客户要到商场购买茶具30套,茶碗![]() 只(
只(![]() ).
).
(1)若客户按方案一,需要付款 元;若客户按方案二,需要付款 元.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,试通过计算说明此时哪种购买方案比较合适?
,试通过计算说明此时哪种购买方案比较合适?
(3)当![]() ,能否找到一种更为省钱的方案,如果能是写出你的方案,并计算出此方案应付钱数;如果不能说明理由.
,能否找到一种更为省钱的方案,如果能是写出你的方案,并计算出此方案应付钱数;如果不能说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com