
【题目】E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】4月12日华为新出的型号为“P30 Pro”的手机在上海召开发布会,某华为手机专卖网店抓住商机,购进10000台“P30 Pro”手机进行销售,每台的成本是4400元,在线同时向国内、国外发售.第一个星期,国内销售每台售价是5400元,共获利100万元,国外销售也售出相同数量该款手机,但每台成本增加400元,获得的利润却是国内的6倍.
(1)求该店销售该款华为手机第一个星期在国外的售价是多少元?
(2)受中美贸易战影响,第二个星期,国内销售每台该款手机售价在第一个星期的基础上降低m%,销量上涨5m%;国外销售每台售价在第一个星期的基础上上涨m%,并且在第二个星期将剩下的手机全部卖完,结果第二个星期国外的销售总额比国内的销售总额多6993万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 以
以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒
秒![]() .
.
![]()
(1)当![]() 时,求线段
时,求线段![]() 和
和![]() 的长度.
的长度.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 中点为
中点为![]() ,则
,则![]() 的长是否变化?若不变.求出
的长是否变化?若不变.求出![]() 的长;若发生变化,请说明理由.
的长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
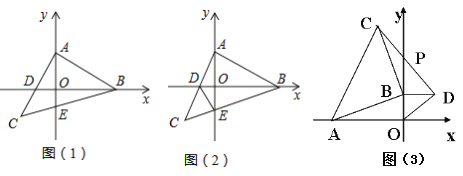
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
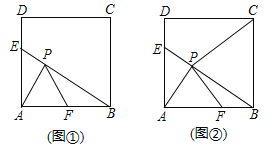
【题目】如图,边长为6的正方形![]() 中,
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 为垂足.
为垂足.
(1)如图①, AF=BF,AE=2![]() ,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
(2)如图②,若![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣![]() ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )
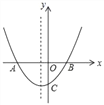
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=5 cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设落点为F,若△ABF的面积为30 cm2,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com