
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
【答案】D
【解析】
A、由a=1>0,可得出抛物线开口向上,A选项错误;
B、由抛物线与y轴的交点坐标可得出c值,进而可得出抛物线的解析式,令y=0求出x值,由此可得出抛物线与x轴的交点为(1,0)、(2,0),B选项错误;
C、由抛物线开口向上,可得出y无最大值,C选项错误;
D、由抛物线的解析式利用二次函数的性质,即可求出抛物线的对称轴为直线x=-![]() ,D选项正确.
,D选项正确.
综上即可得出结论.
解:A、∵a=1>0,
∴抛物线开口向上,A选项错误;
B、∵抛物线y=x2-3x+c与y轴的交点为(0,2),
∴c=2,
∴抛物线的解析式为y=x2-3x+2.
当y=0时,有x2-3x+2=0,
解得:x1=1,x2=2,
∴抛物线与x轴的交点为(1,0)、(2,0),B选项错误;
C、∵抛物线开口向上,
∴y无最大值,C选项错误;
D、∵抛物线的解析式为y=x2-3x+2,
∴抛物线的对称轴为直线x=-![]() =-
=-![]() =
=![]() ,D选项正确.
,D选项正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COB的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
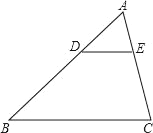
【题目】如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
![]()

(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24 g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
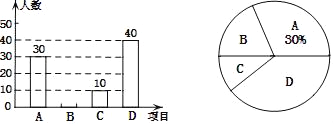
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
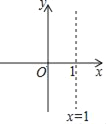
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
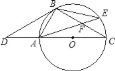
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)根据你的判断:BD是⊙O的切线吗?为什么?.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为10,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
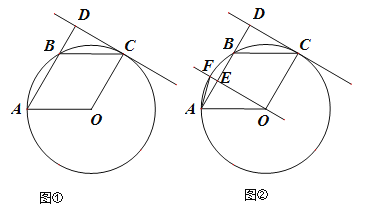
【题目】(本小题10分)已知A, B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(Ⅰ)如图①,求∠ADC的大小;
(Ⅱ)如图②,经过点O作CD的平行线,与AB交于点E,与![]() 交于点F,连接AF,求∠FAB的大小.
交于点F,连接AF,求∠FAB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以点P为圆心,3为半径作⊙P,连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com