【题目】小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（ ）
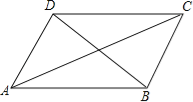
A. ①② B. ②③ C. ①③ D. ②④
【答案】B
【解析】试题分析：A、∵四边形ABCD是平行四边形，当①AB=BC时，平行四边形ABCD是菱形，
当②∠ABC=90°时，菱形ABCD是正方形，故此选项正确，不合题意；B、∵四边形ABCD是平行四边形，
∴当②∠ABC=90°时，平行四边形ABCD是矩形，当AC=BD时，这是矩形的性质，无法得出四边形ABCD是正方形，故此选项错误，符合题意；C、∵四边形ABCD是平行四边形，当①AB=BC时，平行四边形ABCD是菱形，当③AC=BD时，菱形ABCD是正方形，故此选项正确，不合题意；D、∵四边形ABCD是平行四边形，∴当②∠ABC=90°时，平行四边形ABCD是矩形，当④AC⊥BD时，矩形ABCD是正方形，故此选项正确，不合题意．故选：C．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】【问题提出】已知∠AOB＝70°，∠AOD＝
∠AOC，∠BOD＝3∠BOC（∠BOC＜45°），求∠BOC的度数．
【问题思考】聪明的小明用分类讨论的方法解决．
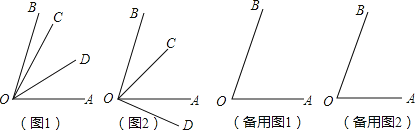
（1）当射线OC在∠AOB的内部时，①若射线OD在∠AOC内部，如图1，可求∠BOC的度数，解答过程如下：
设∠BOC＝α，∴∠BOD＝3∠BOC＝3α，∴∠COD＝∠BOD﹣∠BOC＝2α，∴∠AOD＝
∠AOC，
∴∠AOD＝∠COD＝2α，∴∠AOB＝∠AOD+∠BOD＝2α+3α＝5α＝70°，∴α＝14°，∴∠BOC＝14°
问：当射线OC在∠AOB的内部时，②若射线OD在∠AOB外部，如图2，请你求出∠BOC的度数；
【问题延伸】（2）当射线OC在∠AOB的外部时，请你画出图形，并求∠BOC的度数．
【问题解决】综上所述：∠BOC的度数分别是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
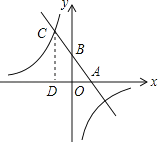
【题目】已知，如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=
（n为常数且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂直为D，若OB=2OA=3OD=6．
（1）求一次函数与反比例函数的解析式；
（2）求两函数图象的另一个交点坐标；
（3）直接写出不等式；kx+b≤
的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线
（m＞0）与x轴的交点为A，B．
（1）求抛物线的顶点坐标；
（2）横、纵坐标都是整数的点叫做整点．
①当m＝1时，求线段AB上整点的个数；
②若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，图象反映的是：小明从家里跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家，其中x表示时间，y表示小明离家的距离．
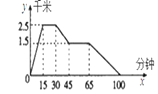
根据图象回答下列问题：
（1）体育场离小明家多远，小明从家到体育场用了多少时间？
（2）体育场离文具店多远？
（3）小明在文具店逗留了多少时间？
（4）小明从文具店回家的平均速度是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
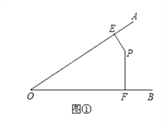
【题目】已知：如图①、②，解答下面各题：
（1）图①中，∠AOB=55°，点P在∠AOB内部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，求∠EPF的度数.
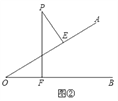
（2）图②中，点P在∠AOB外部，过点P作PE⊥OA，PF⊥OB，垂足分别为E、F，那么∠P与∠O有什么关系？为什么？
（3）通过上面这两道题，你能说出如果一个角的两边分别垂直于另一个角的两边，则这两个角是什么关系？（说明结果，不需要过程）
（4）如果一个角的两边分别平行于另一个角的两边，则这两个角是什么关系？（请画图说明结果，不需要过程）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com