
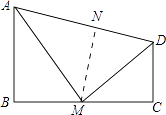
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证: 
(1)AM⊥DM;
(2)M为BC的中点.
【答案】
(1)解:∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM
(2)解:作NM⊥AD交AD于N,
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
【解析】(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.3a3+ a 3=4 a 6B.( a +b)2= a 2+b2C.5 a-5 a =0 D.(-a)2·a 3=-a 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
6月1日 | 12双 | 8双 | 2240元 |
6月2日 | 8双 | 10双 | 1960元 |
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
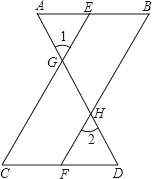
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(_______)
∴∠2=∠CGD(等量代换)
∴CE∥BF(_______)
∴∠_____=∠BFD(_______)
又∵∠B=∠C(已知)
∴∠BFD=∠B(等量代换)
∴AB∥CD(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
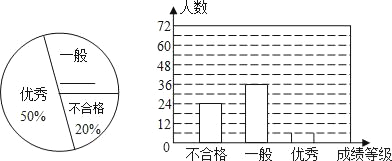
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF. 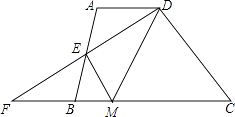
(1)求证:△ADE≌△BFE.
(2)如果FM=CM,求证:EM垂直平分DF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com