练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    根据等式和不等式的基本性质，我们可以得到比较两数大小的方法，若A-B>0，则A>B；若A-B=0，则A=B；若A-B＜0，则A＜B。这种比较大小的方法称为“作差法比较大小”，请运用这种方法尝试解决下列问题。
    （1）比较3a2-2b+1与5+3a2-2b+b2的大小；
    （2）比较a+b与a-b的大小；
    （3）比较3a+2b与2a+3b的大小。
    解：（1）3a2-2b+1-5-3a2+2b-b2=-b2-4＜0
    ∴3a2-2b+1＜5+3a2-2b+b2
    （2）a+b-（a-b）=a+b-a+b=2b，当b>0时，a+b-（a-b=2b>0，
    ∴a+b>a-b
    当b=0时，a+b-（a-b）=2b=0，
    ∴a+b=a-b，当b＜0时，a+b-（a-b）=2b＜0，
    ∴a+b＜a-b。
    （3）3a+2b-（2a+3b）=a-b
    当a>b时，3a+2b>2a+3b
    当a =b时，3a+2b=2a+3b时；
    当a＜b，3a+2b＜2a+3b。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    配方法是数学中一种重要的恒等变形的方法，它的应用十分非常广泛，在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它．下面我们就求函数的极值，介绍一下配方法．
    例：已知代数式a2+6a+2，当a=
    -3
    -3
    时，它有最小值，是
    -7
    -7
    ．
    解：a2+6a+2=a2+6a+9-9+2=（a+3）2-9+2=（a+3）2-7
    因为（a+3）2≥0，所以（a+3）2-7≥-7．
    所以当a=-3时，它有最小值，是-7．
    参考例题，试求：
    （1）填空：当a=
    3
    3
    时，代数式（a-3）2+5有最小值，是
    5
    5
    ．
    （2）已知代数式a2+8a+2，当a为何值时，它有最小值，是多少？

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　八年级数学　下　(北京师大版课标本) 北京师大版课标本 题型：044

    某食品研究部门欲将甲、乙、丙三种食物混合研制成100 kg的食品，并规定：研制成的混合食品中至少需要44000单位维生素A和48000单位维生素B，三种食物维生素A、B的含量如表1所示．

    设所取甲、乙、丙三种食物的质量分别为x kg、y kg、z kg．

    (1)试根据题意列出等式和不等式．

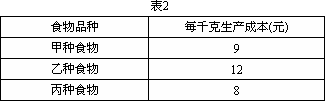
    (2)设甲、乙、丙三种食物生产成本如表2所示．

    ①试用含x、y、z的代数式表示研制混合食品的总成本p；

    ②如果研制混合食品总成本不超过950元，那么你能写出x，y应满足的不等式吗？

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　八年级数学　下　(北京师大版课标本) 北京师大版课标本 题型：044

    某食品研究部门欲将甲、乙、丙三种食物混合研制成100 kg的食品，并规定：研制成的混合食品中至少需要44000单位维生素A和48000单位维生素B，三种食物维生素A、B含量如表1所示：

    设所取甲、乙、丙三种食物的质量分别为x kg、y kg、z kg．

    (1)试根据题意列出等式和不等式，并说明：

    ①y≥20；

    ②2x－y≥40．

    (2)设甲、乙、丙三种食物的生产成本如表2所示：

    ①试用含x、y的代数式表示研制混合食品的总成本p；

    ②若限定混合食物中甲种食物的质量为40 kg，试求此时成本p的取值范围，并确定当p取最小值时，所取乙、丙两种食物的质量．

    查看答案和解析>>

    科目：初中数学 来源：中考备考专家数学(第二版) 题型：044

    先阅读下列一段文字，然后解答问题．

    某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食品，并规定：研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B．三种食物维生素A、B的含量如表所示．

    设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克．试根据题意列出等式和不等式，并证明：

    (1)y≥20；(2)2x－y≥40．

    查看答案和解析>>

    同步练习册答案