
(本小题10分)在平面直角坐标系中,将直线l: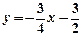 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线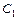 :
: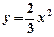 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线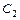 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线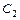 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
解:(1)设直线AB的解析式为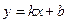 .
.
将直线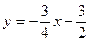 与x轴、y轴交点分别为(-2,0),(0,
与x轴、y轴交点分别为(-2,0),(0,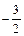 ),
),
沿x轴翻折,则直线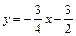 、直线AB
、直线AB
与x轴交于同一点(-2,0),
∴A(-2,0).
与y轴的交点(0,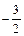 )与点B关于x轴对称,
)与点B关于x轴对称,
∴B(0,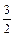 ),
),
∴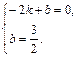
解得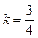 ,
,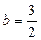 .
.
∴直线AB的解析式为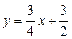 .·························································· 3分
.·························································· 3分
(2)设平移后的抛物线 的顶点为P(h,0),
的顶点为P(h,0), 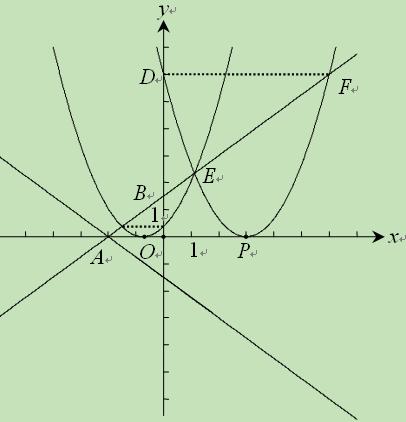
则抛物线 解析式为:
解析式为: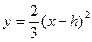 =
=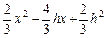 .
.
∴D(0,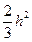 ). ………4分
). ………4分
∵DF∥x轴,
∴点F(2h,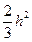 ), ………5分
), ………5分
又点F在直线AB上,
∴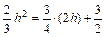 . ………6分
. ………6分
 解得
解得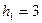 ,
,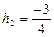 .
.
∴抛物线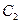 的解析式为
的解析式为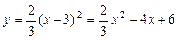 或
或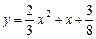 .………7分
.………7分
(3)过M作MT⊥FH于T,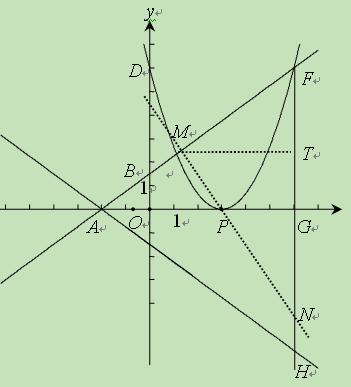
∴Rt△MTF∽Rt△AGF.
∴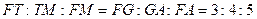 .
.
设FT=3k,TM=4k,FM=5k.
则FN=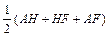 -FM=16-5k.……………8分
-FM=16-5k.……………8分
∴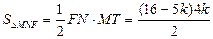 .
.
∵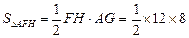 =48,
=48,
又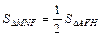 .
.
∴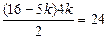 .
.
解得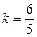 或
或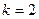 (舍去).
(舍去).
∴FM=6,FT=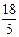 ,MT=
,MT=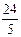 ,GN=4,TG=
,GN=4,TG=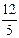 .
.
∴M(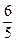 ,
,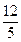 )、N(6,-4).
)、N(6,-4).
∴直线MN的解析式为: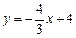 .······················································ 10分
.······················································ 10分
解析


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
(本小题10分)在平面直角坐标系中,将直线l: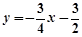 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线:
 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
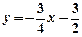 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线 :
: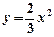 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线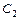 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F. 的解析式;
的解析式;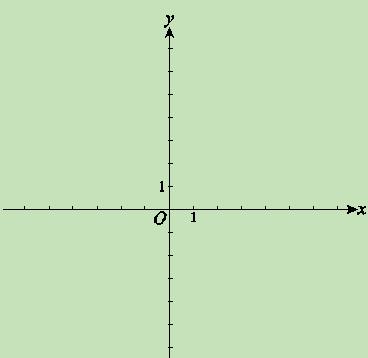
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖南娄底卷)数学 题型:解答题
(本小题10分)在等腰梯形ABCD中,AD∥BC,且AD=2,以CD为直径作⊙
O1,交BC于点E,过点E作EF⊥AB于F,建立如图12所示的平面直角坐标系,已知A,
B两点的坐标分别为A(0,2 ),B(-2,0).
),B(-2,0).
(1)求C,D两点的坐标.
(2)求证:EF为⊙O1的切线.
(3)探究:如图13,线段CD上是否存在点P,使得线段PC的长度与P点到y轴的距离相等?如果存在,请找出P点的坐标;如果不存在,请说明理由.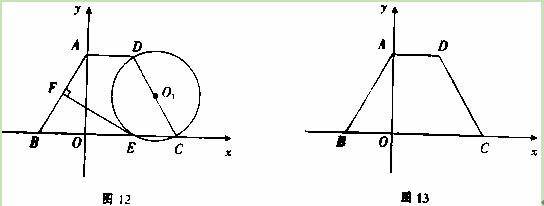
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北十堰卷)数学 题型:解答题
(本小题10分)
在平面直角坐标系中,将直线l: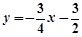 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线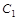 :
: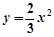 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线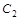 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线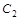 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com