
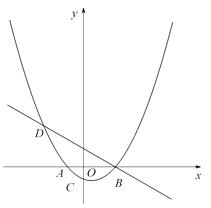
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœfl![]() (aŒ™≥£ ˝£¨«“a£æ0)”Îx÷·¥”◊Û÷¡”““¿¥ŒΩª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨æ≠π˝µ„Bµƒ÷±œfl
(aŒ™≥£ ˝£¨«“a£æ0)”Îx÷·¥”◊Û÷¡”““¿¥ŒΩª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨æ≠π˝µ„Bµƒ÷±œfl![]() ”Î≈◊ŒÔœflµƒ¡Ì“ªΩªµ„Œ™D£¨«“µ„Dµƒ∫·◊¯±ÍŒ™©Å5£Æ
”Î≈◊ŒÔœflµƒ¡Ì“ªΩªµ„Œ™D£¨«“µ„Dµƒ∫·◊¯±ÍŒ™©Å5£Æ
£®1£©«Û≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©PŒ™÷±œflBDœ¬∑Ωµƒ≈◊ŒÔœfl…œµƒ“ªµ„£¨¡¨Ω”PD°¢PB, «Û°˜PBD√ʪ˝µƒ◊Ó¥Û÷µ£Æ
£®3£©…ËFŒ™œfl∂ŒBD…œ“ªµ„(≤ª∫¨∂Àµ„)£¨¡¨Ω”AF£¨“ª∂ص„M¥”µ„A≥ˆ∑¢£¨—ÿœfl∂ŒAF“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩF£¨‘Ÿ—ÿœfl∂ŒFD“‘√ø√Î2∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩD∫ÛÕ£÷𣨵±µ„Fµƒ◊¯±Í «∂‡…Ÿ ±£¨µ„M‘⁄’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£ø
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©µ±F◊¯±ÍŒ™(£≠2£¨
£ª£®3£©µ±F◊¯±ÍŒ™(£≠2£¨ ![]() ) ±£¨µ„M‘⁄’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£Æ
) ±£¨µ„M‘⁄’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ: (1£© ◊œ»«Û≥ˆµ„A°¢B◊¯±Í£¨»ª∫Û«Ûµ√µ„D◊¯±Í£¨¥˙»Î≈◊ŒÔœfly=a£®x+2£©£®x-4£©£®aŒ™≥£ ˝£¨«“a£æ0£©£¨«Ûµ√≈◊ŒÔœflΩ‚Œˆ Ω£ª
(2) …ËP(m, ![]() ),∏˘æ›»˝Ω«–Œµƒ√ʪ˝π´ Ωº¥ø…µ√Ω‚£ª
),∏˘æ›»˝Ω«–Œµƒ√ʪ˝π´ Ωº¥ø…µ√Ω‚£ª
£®3£©”…“‚£¨∂ص„M‘À∂صƒ¬∑æ∂Œ™’€œflAF+DF£¨‘À∂Ø ±º‰£∫t=AF+![]() DF£Æ◊˜∏®÷˙œfl£¨Ω´AF+
DF£Æ◊˜∏®÷˙œfl£¨Ω´AF+![]() DF◊™ªØŒ™AF+FG£ª‘Ÿ”…¥πœfl∂Œ◊Ó∂㨵√µΩ¥πœfl∂ŒAH”Î÷±œflBDµƒΩªµ„£¨º¥Œ™À˘«ÛµƒFµ„£Æ
DF◊™ªØŒ™AF+FG£ª‘Ÿ”…¥πœfl∂Œ◊Ó∂㨵√µΩ¥πœfl∂ŒAH”Î÷±œflBDµƒΩªµ„£¨º¥Œ™À˘«ÛµƒFµ„£Æ
‘Ã‚Ω‚Œˆ£∫(1)≈◊ŒÔœfl![]() ¡Óy£Ω0£¨Ω‚µ√x£Ω£≠2ªÚx£Ω4£¨
¡Óy£Ω0£¨Ω‚µ√x£Ω£≠2ªÚx£Ω4£¨
°‡A(£≠2£¨0)£¨B(4£¨0)£Æ
°fl÷±œfl![]() æ≠π˝µ„B(4£¨0)£¨
æ≠π˝µ„B(4£¨0)£¨
°‡![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°‡÷±œflBDΩ‚Œˆ ΩŒ™£∫ ![]() £Æ
£Æ
µ±x£Ω£≠5 ±£¨y£Ω3![]() £¨
£¨
°‡D(£≠5£¨3![]() )£Æ
)£Æ
°flµ„D(£≠5£¨ ![]() )‘⁄≈◊ŒÔœfl
)‘⁄≈◊ŒÔœfl![]() …œ£¨
…œ£¨
°‡![]() £¨
£¨
°‡![]() £Æ
£Æ
°‡≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô ΩŒ™£∫ ![]() £Æ
£Æ
(2)…ËP(m, ![]() )
)
°‡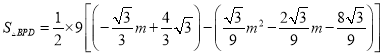
![]() £Æ
£Æ ![]()
°‡°˜BPD√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() £Æ£Æ
£Æ£Æ
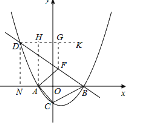
(3)◊˜DK°ŒAB£¨AH°ÕDK£¨AHΩª÷±œflBD”⁄µ„F£¨
°fl”…(2)µ√£¨DN£Ω![]() ,BN£Ω9£¨»›“◊µ√°œDBA£Ω30°„£¨°‡°œBDH£Ω30°„£¨
,BN£Ω9£¨»›“◊µ√°œDBA£Ω30°„£¨°‡°œBDH£Ω30°„£¨
°‡FG£ΩDF°¡sin30°„£Ω![]() £¨
£¨
°‡µ±«“Ωˆµ±AH°ÕDK ±£¨AF+FH◊Ó–°£¨
µ„M‘⁄’˚∏ˆ‘À∂Ø÷–”√ ±Œ™£∫t£Ω![]() £¨
£¨
°fllBD£∫ ![]() £¨°‡Fx£ΩAx£Ω£≠2£¨F(£≠2£¨
£¨°‡Fx£ΩAx£Ω£≠2£¨F(£≠2£¨ ![]() )
)
°‡µ±F◊¯±ÍŒ™(£≠2£¨ ![]() ) ±£¨”√ ±◊Ó…Ÿ£Æ
) ±£¨”√ ±◊Ó…Ÿ£Æ


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™“ª∏ˆ»˝Ω«–Œµƒ¡Ω±fl≥§∑÷± «4∫Õ8£¨»Ù»˝Ω«–Œ «µ»—¸»˝Ω«–Œ£¨ƒ«√¥÷‹≥§ «____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨Àƒ±fl–ŒABCDÀƒÃı±fl…œµƒ÷–µ„∑÷±Œ™E°¢F°¢G°¢H£¨À≥¥Œ¡¨Ω”EF°¢FG°¢GH°¢HE£¨µ√µΩÀƒ±fl–ŒEFGH£®º¥Àƒ±fl–ŒABCDµƒ÷–µ„Àƒ±fl–Œ£©£Æ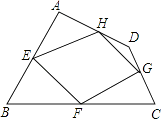
£®1£©Àƒ±fl–ŒEFGHµƒ–Œ◊¥ « £¨ ≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
£®2£©µ±Àƒ±fl–ŒABCDµƒ∂‘Ω«œfl¬˙◊„Ãıº˛ ±£¨Àƒ±fl–ŒEFGH «æÿ–Œ£ª
£®3£©ƒ„—ßπ˝µƒƒƒ÷÷Ãÿ ‚Àƒ±fl–Œµƒ÷–µ„Àƒ±fl–Œ «æÿ–Œ£ø
£®4£©µ±Àƒ±fl–ŒABCDµƒ∂‘Ω«œfl¬˙◊„Ãıº˛ ±£¨Àƒ±fl–ŒEFGH «¡‚–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄°˜ABC÷–£¨CD «AB±fl…œµƒ∏fl£¨AC=4£¨BC=3£¨DB= ![]() £¨«Û£∫
£¨«Û£∫ 
£®1£©«ÛADµƒ≥§£ª
£®2£©°˜ABC «÷±Ω«»˝Ω«–Œ¬£øŒ™ ≤√¥£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
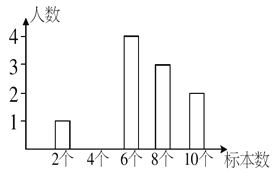
°æƒø°øƒ≥…˙ŒÔøŒÕ‚ªÓ∂Ø–°◊ȵƒÕ¨—ß柖–÷≤ŒÔ±Í±æ÷∆◊˜±»»¸£¨Ω·π˚Õ≥º∆»Áœ¬£∫

∏˘æ›±Ì÷–Ã·π©µƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©∏√◊Èπ≤”–—ß…˙∂‡…Ÿ»À£ø
£®2£©√ø»À÷∆◊˜±Í±æ ˝‘⁄6∏ˆº∞“‘…œµƒ»À ˝‘⁄»´◊È»À ˝÷–À˘’º±»¿˝£ø
£®3£©∆Ωæ˘√ø»À÷∆◊˜∂‡…Ÿ∏ˆ±Í±æ£ø
£®4£©≤π»´œ¬ÕºµƒÃı–ŒÕ≥º∆Õº£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù©Å2x2y£®©Åxmy+3xy3£©=2x5y2©Å6x3yn £¨ ‘Úm= £¨ n= £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø’˝∑Ω–ŒABCD÷–£¨AB=4£¨∂‘Ω«œflΩª”⁄µ„O£¨F «BOµƒ÷–µ„£¨¡¨Ω”AF£¨«ÛAFµƒ≥§∂»£Æ 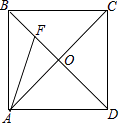
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ ˝÷·…œA°¢B°¢C»˝µ„±Ì 浃 ˝∑÷±Œ™![]() °¢
°¢![]() °¢
°¢![]() £¨«“
£¨«“![]() °¢
°¢![]() ¬˙◊„
¬˙◊„![]() £Æ
£Æ
![]()
(1)‘Ú![]() = £¨
= £¨ ![]() = £ª
= £ª
(2)∂ص„P¥”Aµ„≥ˆ∑¢£¨“‘√ø√Î10∏ˆµ•ŒªµƒÀŸ∂»—ÿ ˝÷·œÚ”“‘À∂Ø£¨µΩ¥ÔBµ„Õ£¡Ù∆¨øÃ∫Û¡¢º¥“‘√ø√Î6∏ˆµ•ŒªµƒÀŸ∂»—ÿ ˝÷·∑µªÿµΩAµ„£¨π≤”√¡À6√Σª∆‰÷–¥”CµΩB£¨∑µªÿ ±¥”BµΩC(∞¸¿®‘⁄Bµ„Õ£¡Ùµƒ ±º‰)π≤”√¡À2√ΣÆ
¢Ÿ«ÛCµ„±Ì 浃 ˝![]() £ª
£ª
¢⁄…Ë‘À∂Ø ±º‰Œ™![]() √Σ¨«Û
√Σ¨«Û![]() Œ™∫Œ÷µ ±£¨µ„PµΩA°¢B°¢C»˝µ„µƒæ‡¿Î÷Æ∫ÕŒ™23∏ˆµ•Œª£ø
Œ™∫Œ÷µ ±£¨µ„PµΩA°¢B°¢C»˝µ„µƒæ‡¿Î÷Æ∫ÕŒ™23∏ˆµ•Œª£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∞—æÿ–ŒABCD—ÿEF∑≠’€£¨µ„B«°∫√¬‰‘⁄AD±flµƒB°‰¥¶£¨»ÙAE=2£¨DE=6£¨°œEFB=60°„£¨‘Úæÿ–ŒABCDµƒ√ʪ˝ «£® £© 
A.12
B.24
C.12 ![]()
D.16 ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com