Question

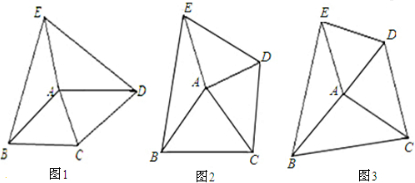
如图① ，在△ABC中，AB=AC=4，∠BAC=90^ｏ，AD⊥BC，垂足为D.
（1）S_△ABD =     .(直接写出结果)
（2）如图②，将△ABD绕点D按顺时针方向旋转得到△A′B′D，设旋转角为 ()，在旋转过程中：
探究一：四边形APDQ的面积是否随旋转而变化？说明理由
探究二：当的度数为多少时，四边形APDQ是正方形？说明理由.

Answer 1

（1）4，（2）①不会；②=45^ｏ

解析试题分析：（1）根据S_△ABD= S_{△AB C}结合三角形的面积公式进行解答即可；
（2）①四边形APDQ的面积不会随旋转而变化，因为无论旋转角为 ()怎样旋转，始终是△BPD≌△AQD，即四边形APDQ的面积等于S_△ABD；
②证得四边形APDQ为矩形，又因为DP=AP=AB，即可得出结论.
（1）S_△ABD=  S_△ABC= =4
（2）① 四边形APDQ的面积不会随旋转而变化.
理由如下：在△ABC中，AB=AC，∠BAC=90^ｏ
∠B=∠C=45^ｏ
∵AD⊥BC
∴∠BAD=∠DAC=45^ｏ
∴∠B="∠DAQ=∠BAD" =45^ｏ，BD=AD
又∵∠BDP+∠ADP=90^ｏ，∠ADQ+∠ADP=∠PDQ=90^ｏ
∴∠BDP="∠ADQ"
∴△BPD≌△AQD
S_{四边形APDQ}= S_△APD+ S_△AQD= S_△APD+ S_△BPD= S_△ABD =4
② 当=45^ｏ时，四边形ＡPDQ是正方形.
理由如下：

由（1）知△ABD为等腰直角三角形.
当=45^ｏ时，DP⊥AB，即∠APD=90^ｏ
又∵∠A=90^ｏ，∠PDQ=90^ｏ
∴四边形APDQ为矩形
又∵DP=AP=AB
∴四边形APDQ是正方形.
考点：旋转的性质，三角形的面积公式，正方形的判定和性质
点评：本题知识点较多，综合性强，难度较大，在中考中比较常见，一般以压轴题形式出现.