
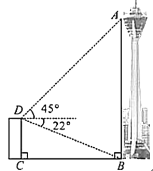
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】观景台的高![]() 约为214米.
约为214米.
【解析】
过点D作DM⊥AB于点M,由题意可得四边形DCBM是矩形,由矩形的性质可得BM=CD=61米;在Rt△BDM中,∠BDM=22°,BM=61米,由此可得tan22°=![]() ,即可求得DM=152.5米;再证明△ADM为等腰直角三角形,可得DM=AM=152.5米,由此即可求得观景台的高
,即可求得DM=152.5米;再证明△ADM为等腰直角三角形,可得DM=AM=152.5米,由此即可求得观景台的高![]() 的长.
的长.
过点D作DM⊥AB于点M,由题意可得四边形DCBM是矩形,
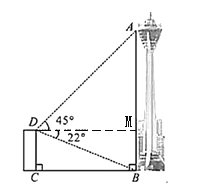
∴BM=CD=61米,
在Rt△BDM中,∠BDM=22°,BM=61米, tan∠BDM=![]() ,
,
∴tan22°=![]() ,
,
解得,DM=152.5米;
∵∠ADM=45°,DM⊥AB,
∴△ADM为等腰直角三角形,
∴DM=AM=152.5米,
∴AB=BM+AM=61+152.5=213.5≈214(米).
答:观景台的高![]() 约为214米.
约为214米.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
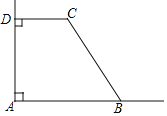
【题目】如图所示,AB⊥AD于点A,CD⊥AD于点D,∠C=120°.若线段BC与CD的和为12,则四边形ABCD的面积可能是( )
A.24![]() B.30
B.30![]() C.45D.
C.45D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=4,边BC在其所在的直线上平移,平移后得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
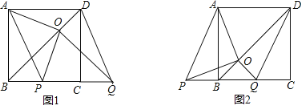
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并利用图1加以证明.
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤4),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到加工粮食任务,要求![]() 天加工完
天加工完![]() 吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量
吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图①所示;未加工粮食
(天)之间的函数关系如图①所示;未加工粮食![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图②所示、请结合图象解答下列问题:
(天)之间的函数关系如图②所示、请结合图象解答下列问题: ![]()
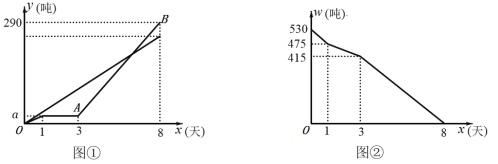
(1)甲车间每天加工粮食 吨,![]() ;
;
(2)求乙车间维修设备后,乙车间加工粮食数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求加工![]() 吨粮食需要几天完成.
吨粮食需要几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
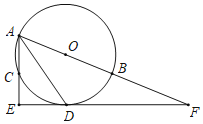
【题目】如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=![]() ,求tan∠EAD的值.
,求tan∠EAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC中AB边上一点,以点O为圆心,OA的长为半径作⊙O,⊙O恰好经过点C,且与边BC,AB分别交于E,F两点.连接AE,过点E作⊙O的切线,交线段BF于点M,交AC的延长线于点N,且EM=BM,EB=AO.
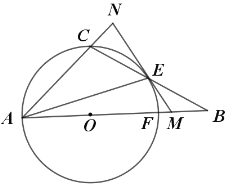
(1)求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于已知的两个函数,任取自变量![]() 的一个值,当
的一个值,当![]() 时,它们对应的函数值相等;当
时,它们对应的函数值相等;当![]() 时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数
时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数![]() ,它的相关函数为
,它的相关函数为![]() .
.
(1)已知点![]() 在一次函数
在一次函数![]() 的相关函数的图像上,求
的相关函数的图像上,求![]() 的值;
的值;
(2)已知二次函数![]() .
.
①当点![]() 在这个函数的相关函数的图像上时,求
在这个函数的相关函数的图像上时,求![]() 的值;
的值;
②当![]() 时,求函数
时,求函数![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
(3)在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,连结
,连结![]() .直接写出线段
.直接写出线段![]() 与二次函数
与二次函数![]() 的相关函数的图像有两个公共点时
的相关函数的图像有两个公共点时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
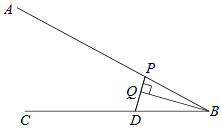
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
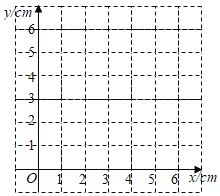
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com