
����Ŀ������֪ѧϰ��
���һ����������һ���ϵ����ߵ��������ߵ�һ�룬��ô���ǾͰ������������ν������ǻ������Ρ���
�������ã�
��1���������������Σ����ǻ������ε���______������ţ���

��2����ͼ����֪�ȱ�������![]() �����ÿ̶ȳ��ڸ������α����ҳ��������������ĵ�
�����ÿ̶ȳ��ڸ������α����ҳ��������������ĵ�![]() ��ʹ
��ʹ![]() Ϊ���ǻ������Ρ�����д��������
Ϊ���ǻ������Ρ�����д��������

������̽����
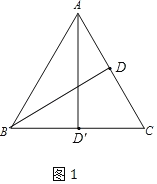
��3����ͼ����������![]() �У���
����![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() �����ж�
�����ж�![]() �Ƿ�Ϊ���ǻ������Ρ�����˵�����ɣ�
�Ƿ�Ϊ���ǻ������Ρ�����˵�����ɣ�

�����Ӧ�ã�
��4����ͼ���ȱ�������![]() �߳�
�߳�![]() ��������
��������![]() ��
��![]() ���ٶȴӵ�
���ٶȴӵ�![]() ��������
��������![]() �ı�
�ı�![]() �˶�������һ����
�˶�������һ����![]() ��
��![]() ���ٶȴӵ�
���ٶȴӵ�![]() �������ر�
�������ر�![]() �˶�������ͬʱ����������
�˶�������ͬʱ����������![]() �״λص���
�״λص���![]() ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊ
ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() ����ô
����ô![]() Ϊ______
Ϊ______![]() ʱ��
ʱ��![]() Ϊ���ǻ������Ρ���
Ϊ���ǻ������Ρ���

���𰸡���1���٣���2�������������3��![]() �ǡ��ǻ������Ρ������������������4��1��
�ǡ��ǻ������Ρ������������������4��1��![]() ��
��![]() ��7
��7
��������
��1������ֱ��������б�����ߵ����ʼ����жϣ�
��2���ÿ̶ȳ߷ֱ���ȡAC��BC���е�D��D'����D��D'��Ϊ����
��3�����ۣ���AEF�ǡ��ǻ������Ρ������ù��ɶ������涨��֤����AEF��ֱ�������μ��ɣ�
��4���ֵ���P���߶�AB�ϣ���Q���߶�BC��ʱ�͵�P���߶�BC�ϣ���Q���߶�AB���������ηֱ�������⼴�ɣ�
��1����Ϊֱ�������ε�б���ϵ����ߵ���б�ߵ�һ�룬���Ԣ��ǡ��ǻ������Ρ���
�ʴ�Ϊ���٣�
��2���ÿ̶ȳ߷ֱ���ȡAC��BC���е�D��D'��
��D��D'������
��3�����ۣ���AEF�ǡ��ǻ������Ρ���
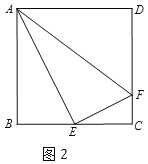
�������£���ͼ���������εı߳�Ϊ4a��
��E��BC���е㣬��BE=EC=2a��
��CF![]() CD����FC=a��DF=4a��a=3a��
CD����FC=a��DF=4a��a=3a��
��Rt��ABE��AE2=��4a��2+��2a��2=20a2
��Rt��ECF��EF2=��2a��2+a2=5a2
��Rt��ADF�У�AF2=��4a��2+��3a��2=25a2����AE2+EF2=AF2�����AEF��ֱ�������Σ���AEF=90�㣮
��ֱ��������б��AF�ϵ����ߵ���AF��һ�룬���AEFΪ���ǻ������Ρ���
��4����ͼ3�У�
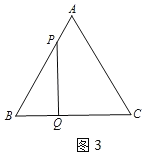
�ٵ���P���߶�AB�ϣ���Q���߶�BC��ʱ������PQB=90�㣬��BP=2BQ����5��t=4t��
��ã�t=1��
����BPQ=90�㣬��BQ=2PB����2t=2��5��t������t![]() ��
��
�ڵ���P���߶�BC�ϣ���Q���߶�AB��ʱ������PQB=90�㣬��BP=2BQ����t��5=2��15��2t������t=7��
����QPB=90�㣬��BQ=2PB����15��2t=2��t��5������t![]() ��
��
��������������������t��ֵΪ1��![]() ��
��![]() ��7��
��7��
�ʴ�Ϊ��1��![]() ��
��![]() ��7��
��7��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
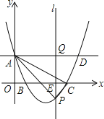
����Ŀ����ͼ,��֪����y=x+2��ͼ����y�ύ�ڵ�A,һ�κ���y=kx+b��ͼ����B(0,4)����x�ἰy=x+2��ͼ��ֱ��ڵ�C��D,��D������Ϊ(![]() ,n)
,n)

(1)��n= ,k= ,b=_______��
(2)������y=kx+b�ĺ���ֵ���ں���y=x+2�ĺ���ֵ,��x��ȡֵ��Χ��_______��
(3)���ı���AOCD�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬ�ĵ���ֱ�����������ǰ���ͼ1��ʾ���ã�ͼ2������������ļ���ͼ�Σ�B��C��E��ͬһ��ֱ���ϣ�����DC��
��1����֤����ABE�ա�ACD��
��2����֤��DC��BE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() ��Ľ���ֱ�Ϊ
��Ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ᣬ��
�ᣬ��![]() ������һ����
������һ����![]() ����
����![]() ��ƽ����
��ƽ����![]() ���ֱ��
���ֱ��![]() �������ߡ�ֱ��
�������ߡ�ֱ��![]() �Ľ���ֱ�Ϊ
�Ľ���ֱ�Ϊ![]() ��
��![]() ��
��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��
��![]() ʱ����
ʱ����![]() ��������ֵ��
��������ֵ��
![]() ��
��![]() ʱ���Ƿ���ڵ�
ʱ���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ������ڣ������ʱ
���ƣ������ڣ������ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�������г���ҵľ���![]() ��ʱ��
��ʱ��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
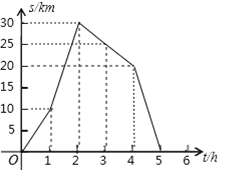
��1��������仯�������Ա�����______���������______��
��2��С���ʱ���������Զ�ĵط�����ʱ��Ҷ�Զ��
��3����ֱ��д��С���ʱ������![]() ��
��
��4�����С����γ��е�ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������������������Ƕ���ʽ�˷�չ��ʽ��ϵ�����ɣ��磺�����е���������1��2��1��ǡ�ö�Ӧ�ţ�a+b��2��չ��ʽa2+2ab+b2��ϵ���������е��ĸ���ǡ�ö�Ӧ�ţ�a+b��3��a3+3a2b+3ab2+b3��ϵ��������������ǰ���е���������ӳ�Ĺ��ɣ��ش�
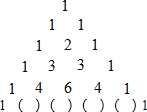
��1��ͼ�е���������������ֱַ����� �������밴�����ҵ�˳����д��
��2����a+b��4���� ����
��3����������Ĺ��ɼ�����ֵ����![]() ��4��4����
��4��4����![]() ��3+6����
��3+6����![]() ��2��4��
��2��4��![]() +1��
+1��
��4������2x��1��2018��a1x2018+a2x2017+a3x2016+����+a2017x2+a2018x+a2019����a1+a2+a3+����+a2017+a2018��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
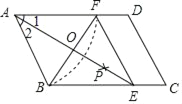
����Ŀ����ͼ����ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��1��������������ͼ��Ϣ֪�ı���ABEF���� ��
A���������ƽ���ı���
B������
C������
D��������
��2����AE��BF�ཻ�ڵ�O���ı���ABEF���ܳ�Ϊ16��BF=4����AE�ij��͡�C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��m��1��x+3��ͼ����x��ĸ������ཻ�ڵ�A����y���ཻ�ڵ�B������OAB���Ϊ![]() .
.

��1����m��ֵ����A�����ꣻ
��2������B��ֱ��BP��x����������ཻ�ڵ�P����OP=2OA����ֱ��BP�ĺ�������ʽ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һԲ�������Ϊ12cm�����ĵ���뾶Ϊ3cm����Բ���µ���A����һֻ���ϣ�����õ�����B����ʳ������Ͼ�������̾���Ϊ_________.����ȡ3��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com