
【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
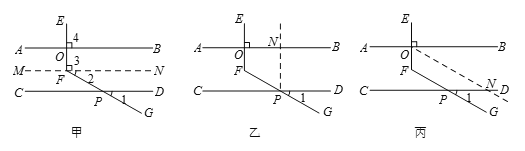
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
【答案】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)120°
【解析】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
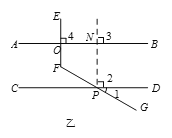
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)过点O作ON∥FG
∵ON∥FG
∴∠EFG=∠EON ∠1=∠ONC=30°
∵AB∥CD
∴∠ONC=∠BON=30°
∵EF⊥AB
∴∠EOB=90°
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
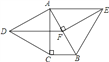
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当![]() =____时,四边形ADFE是平行四边形.
=____时,四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2的图象向右平移2个单位,得到新的函数图像的表达式是( )
A. y=x2-2 B. y=(x-2)2 C. y=x2+2 D. y=(x+2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,正确的是( )
A. (a+b)2=a2+b2 B. (﹣x﹣y)2=x2+2xy+y2
C. (x+3)(x﹣2)=x2﹣6 D. (﹣a﹣b)(a+b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
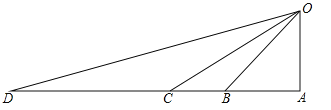
【题目】“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7).
≈1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线a平行于x轴,点M(-2,-3)是直线a上的一个点.若点N也是直线a上的一个点,请写出符合条件的一个点N的坐标,N________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com