
 如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.分析 (1)根据三角形的重心的性质得到CP=2OP,根据平行线分线段成比例定理、正切的概念计算即可;
(2)设正方形的边长为a,求出EF、BP,根据三角形的面积公式计算即可.
解答 解:(1)∵点O是△BEF的重心,
∴OB=2OP,
则点P是OC的中点,
∵EF∥AD,
∴点E是AD的中点,
∴tan∠ABE=$\frac{AE}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$;
(2)设正方形的边长为a,
则BC=$\sqrt{2}$a,
∴EF=$\frac{1}{2}$AD=$\frac{\sqrt{2}}{2}$a,BP=$\frac{3\sqrt{2}}{4}$a,
∴$\frac{{S}_{△BEF}}{{S}_{正方形ABCD}}$=$\frac{\frac{1}{2}×\frac{\sqrt{2}}{2}a×\frac{3\sqrt{2}}{2}a}{{a}^{2}}$×$\frac{1}{2}$=$\frac{3}{8}$.
点评 本题考查的是三角形的重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.


科目:初中数学 来源: 题型:填空题
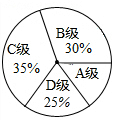 为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.
为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
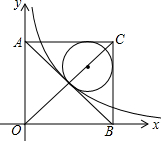 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
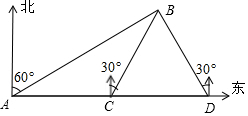 如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.
如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
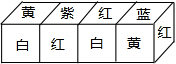 把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com