
����Ŀ����ͼ�٣���֪������y=ax2+bx+3��a��0����x�ύ�ڵ�A��1��0���͵�B��-3��0������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�����x�ύ�ڵ�M�����ڶԳ������Ƿ���ڵ�P��ʹ��CMPΪ���������Σ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ�ڣ�����EΪ�ڶ�������������һ���㣬����BE��CE�����ı���BOCE��������ֵ�������ʱE������꣮
���𰸡���1��y=-x2-2x+3����2�����ڣ�P��-1��![]() ����P��-1��-
����P��-1��-![]() ����P��-1��6����P��-1��
����P��-1��6����P��-1��![]() ������3����a=-
������3����a=-![]() ʱ��S�ı���BOCE��������ֵΪ
ʱ��S�ı���BOCE��������ֵΪ![]() ����ʱ����E����Ϊ��-
����ʱ����E����Ϊ��-![]() ��
��![]() ����
����
��������
��1����֪�����߹�A��B���㣬�ɽ������������������ߵĽ���ʽ�У��ô���ϵ��������������κ����Ľ���ʽ��
��2���ɸ��ݣ�1���ĺ�������ʽ�ó������ߵĶԳ��ᣬҲ�͵ó���M������꣬����C����������y��Ľ��㣬���C������Ϊ��0��3��������M��C����������CM�ľ��룮Ȼ�����������������ۣ�
�ٵ�CP=PMʱ��Pλ��CM�Ĵ�ֱƽ�����ϣ���P������ؼ�����P�������꣬��P��PQ��y����Q�������PM=CP=x����ôֱ��������CPQ��CP=x��OM�ij����ɸ���M������ó���CQ=3-x����˿ɸ��ݹ��ɶ������x��ֵ��P��ĺ�������M�ĺ�������ͬ��������Ϊx���ɴ˿ɵó�P�����꣮
�ڵ�CM=MPʱ������CM�ij��������P�������꣬Ҳ�͵ó���P�����꣨Ҫע����������㣩��
�۵�CM=CPʱ����ΪC������Ϊ��0��3������ôֱ��y=3�ش�ֱƽ��PM�����P����������6���ɴ˿ɵó�P�����ꣻ
��3�������ı���BOCE���ǹ�����ı��Σ���˿ɽ��ı���BOCE�ָ�ɹ����ͼ�ν��м��㣬��E��EF��x����F��S�ı���BOCE=S��BFE+S����FOCE��ֱ������FOCE�У�FOΪE�ĺ�����ľ���ֵ��EFΪE�������꣬��֪C�������꣬��֪����OC�ij����ڡ�BFE�У�BF=BO-OF����˿���E�ĺ������ʾ��BF�ij�������������������E�����꣬Ȼ�����������߶��У����ɵó������ı���BOCE�������E�ĺ�����ĺ�����ϵʽ�����ݺ��������ʼ�������ı���BOCE�����ֵ����Ӧ��E�ĺ������ֵ�����������ʱE�����꣮
(1)��������y=ax2+bx+3(a��0)��x�ύ�ڵ�A(1,0)�͵�B(3,0)��
��![]()
��ã�![]() .
.
�����������߽���ʽΪ��y=x22x+3��
(2)�������߽���ʽΪ��y=x22x+3��
����Գ���Ϊ![]() ��
��
����P������Ϊ(1,a)����x=0ʱ��y=3��
��C(0,3),M(1,0)
�൱CP=PMʱ,(1)2+(3a)2=a2,���a=![]() ��
��
��P��������![]() ��
��
�൱CM=PMʱ,(1)2+32=a2,���![]() ��
��
��P��������![]() ��
��![]() ��
��
�൱CM=CPʱ,�ɹ��ɶ����ã�(1)2+32=(1)2+(3a)2�����a=6��
��P��������P4 (1,6).

�����������ڷ��������ĵ�P,������Ϊ![]() ��
�� ![]() ��P(1,6)��
��P(1,6)��![]() ��
��
(3)����E��EF��x���ڵ�F,��E(a,a22a+3)(3<a<0)

��EF=a22a+3��BF=a+3��OF=a
��![]()
![]()
![]()

�൱a=![]() ʱ,S�ı���BOCE���,�����ֵΪ
ʱ,S�ı���BOCE���,�����ֵΪ![]() .
.
��ʱ,��E����Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
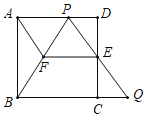
����Ŀ����ͼ���ڱ߳�Ϊl��������ABCD�У�E�DZ�CD���е㣬��P�DZ�AD��һ�㣨���A��D���غϣ�������PE��BC���ӳ��߽��ڵ�Q��
��1����֤��![]() ��
��
��2������E��![]() ��PB�ڵ�F������AF����
��PB�ڵ�F������AF����![]() ʱ������֤���ı���AFEP��ƽ���ı��Σ�
ʱ������֤���ı���AFEP��ƽ���ı��Σ�
�����ж��ı���AFEP�Ƿ�Ϊ���Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪tan��MON=2������ABCD�ı�AB������OM�ϣ�AD=2��AB=m��CF��ON������Ϊ��F.
��1����ͼ��1������AE��ON������Ϊ��E. ��m=2ʱ�����߶�EF�ij��ȣ�
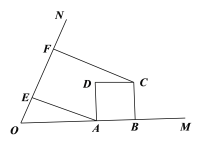
ͼ��1��
��2����ͼ��2��������OC����m=2����CDƽ�֡�FCOʱ�����COF������ֵ��
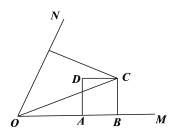
ͼ��2��
��3����ͼ��3��������AFD���CDF����ʱ����m��ֵ.
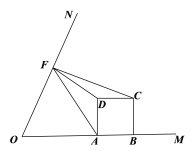
ͼ��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
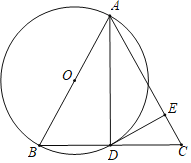
����Ŀ����ͼ����ABC�У�AB=AC��AB�ǡ�O��ֱ����BC���O���ڵ�D����E��AC�ϣ��ҡ�ADE=��B��
��1����֤��DE�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ5��CE=2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��������ABCD��CD��������һ�㣮
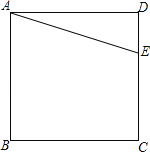
��1���Ե�AΪ���ģ�����ADE˳ʱ����ת90����������ת���ͼ�Σ�
��2����BC���ϻ�һ��F��ʹ��CFE���ܳ�����������ABCD���ܳ���һ�룬���Ҫ˵����ȡ�õ�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ΪԲ�ε����������ֻ������һ���Ƭ������ѧ��ϣ���ܰѴ˼�������и�ԭ����˰Ѳ�Ƭ�������һ�����Σ���ͼ��ʾ�����������õ����θ�CD��![]() �ף���CAD��30���������������ѧ����������������
�ף���CAD��30���������������ѧ����������������
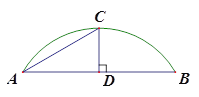
��1����������������Բ��O��λ�ã��߹���ͼ��������ͼ�ۼ�����д��������
��2�������������Բ�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ����Բ�������ߵ�һ������ɵķ��ͼ�γ�Ϊ����Բ����
��ͼ��������y��x2��2x��3��x�ύ�ڵ�A��B����y�ύ�ڵ�D����ABΪֱ������x���Ϸ�����Բ��y���ڵ�C����Բ��Բ�ļ�ΪM����ʱ�����Բ������������x���·�������ɵ�ͼ�ξͳ�Ϊ����Բ����
��1��ֱ��д����A��B��C�����꼰����Բ����CD�ij���
A�� ����B�� ����C�� ����CD���� ����
��2�����һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ�
������C�ġ���Բ�����ߵĽ���ʽ��
������D�ġ���Բ�����ߵĽ���ʽ��
��3���ɣ�2����ù���D�ġ���Բ��������x�ύ���ΪE����F�ǡ���Բ����һ���㣬�����Ƿ����S��CDE��S��CDF���������������F�����ꣻ�������ڣ���˵�����ɣ�
��4����P�ǡ���Բ����һ�㣬�������BPC��60�㣬��BP���ʱ����ֱ��д����P�����꣮
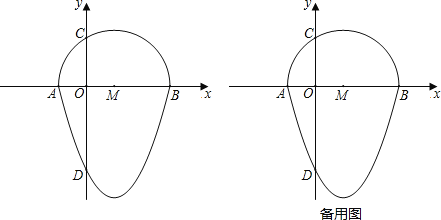
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������˾�ƻ�����A�ͺ�B�����ֽ���������������A������4����B������7��������310��Ԫ��������A������10����B������15��������700��Ԫ��
��1��A�ͺ�B������ÿ���ļ۸�ֱ��Ƕ�����Ԫ��
��2���ù�˾�ƻ�����A�ͺ�B������������10�������ò�����285��Ԫ����A����������������B���������������������������ʡ�ķ�����������÷���������ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ڵ�һ����
��ͼ���ڵ�һ����![]() ��
��![]() ���㣬�������ύ��
���㣬�������ύ��![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() .
.
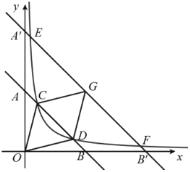
��1����![]() ��
��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����ֱ��![]() ����ƽ��
����ƽ��![]() ����λ��ֱ��
����λ��ֱ��![]() ����ʱ��ֱ��
����ʱ��ֱ��![]() ��ǡ��һ��
��ǡ��һ��![]() ����
����![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com