练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．两个一次函数y1=ax+b，y2=bx+a，它们在同一直角坐标系中大致的图象是（　　）
    A．B．C．D．

    分析 分析四个选项，根据一次函数图象与系数的关系得出a、b的正负，由此即可得出结论．

    解答 解：A、根据y1的函数图象可知：a＞0，b＞0，
    根据y2的函数图象可知：b＜0，a＞0，
    ∴A不正确；
    B、根据y1的函数图象可知：a＜0，b＞0，
    根据y2的函数图象可知：b＞0，a＜0，
    ∴B正确；
    C、根据y1的函数图象可知：a＜0，b＞0，
    根据y2的函数图象可知：b＞0，a＞0，
    ∴C不正确；
    D、根据y1的函数图象可知：a＜0，b＜0，
    根据y2的函数图象可知：b＜0，a＞0，
    ∴D不正确；
    故选B．

    点评 本题考查了一次函数图象与系数的关系，解题的关键是根据一次函数图象与系数的关系分析四个选项中两函数解析式中a、b的正负是否一致．本题属于基础题，难度不大，解决该题型题目时，根据一次函数的图象结合一次函数图象与系数的关系找出系数的正负是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

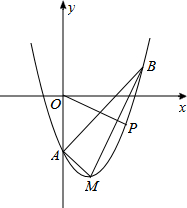    5．如图，在平面直角坐标系xOy中，顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的，它与y轴负半轴交于点A，点B在该抛物线上，且横坐标为3．
    （1）求点M、A、B坐标；
    （2）连结AB、AM、BM，求∠ABM的正切值；
    （3）点P是顶点为M的抛物线上一点，且位于对称轴的右侧，设PO与x正半轴的夹角为α，当α=∠ABM时，求P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知2m+5n+3=0，则4m×32n的值为$\frac{1}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，抛物线y=ax2-2ax+8分别交x轴于点A，B（点A在点B左侧），交y轴于点C，AB=6．
    （1）求a的值；
    （2）点D为抛物线的顶点，点Q在线段BD上，过点Q作QH⊥x轴于点H，在HQ的延长线上取点N，连接BN，在x轴上点H的左侧取点M，连接QM，且MH=6，若tan∠NBH-tan∠MQH=3，求QN的长；
    （3）在（2）的条件下，在AD上取点P，使得AP=DQ，若∠DPQ+∠PQB=90°，求点P的坐标，并判断此时点N是否在抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．我市某中学今年年初开学后打算招聘一名数学教师，对三名前来应聘的数学教师A、B、C进行了考核，他们的笔试成绩和说课成绩（单位：分）分别用了两种方式进行了统计，如表一和图一：
    表一：
     ABC
    笔试859590
    说课8085
    （1）请将表一和图一中的空缺部分补充完整．
    （2）应聘的最后一个程序是由该校的24名数学教师进行投票，三位应聘人的得票情况如图二（没有弃权票，该校的每位教师只能选一位应聘教师），请计算每人的得票数（得票数可是整数哟）．
    （3）若每票计1分，该校将笔试、说课、得票三项测试得分按3：4：4的比例确定个人成绩，请计算三位应聘人的最后成绩，并根据成绩判断谁能应聘成功．

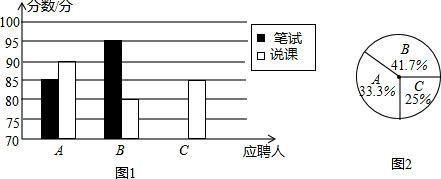
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$，其结果是（　　）
    A．-2B．2C．-$\frac{2（a-2）}{a+2}$D．$\frac{2}{（a+2）^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

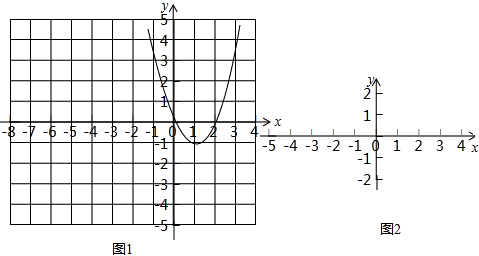    6．在平面直角坐标系 xOy中，对于点P（x，y），以及两个无公共点的图形W1和W2，若在图形W1和W2上分别存在点M （x1，y1 ）和N （x2，y2 ），使得P是线段MN的中点，则称点M 和N被点P“关联”，并称点P为图形W1和W2的一个“中位点”，此时P，M，N三个点的坐标满足x=$\frac{{{x_1}+{x_2}}}{2}$，y=$\frac{{{y_1}+{y_2}}}{2}$
    （1）已知点A（0，1），B（4，1），C（3，-1），D（3，-2），连接AB，CD．
    ①对于线段AB和线段CD，若点A和C被点P“关联”，则点P的坐标为（$\frac{3}{2}$，0）；
    ②线段AB和线段CD的一“中位点”是Q （2，-$\frac{1}{2}$），求这两条线段上被点Q“关联”的两个点的坐标；
    （2）如图1，已知点R（-2，0）和抛物线W1：y=x2-2x，对于抛物线W1上的每一个点M，在抛物线W2上都存在点N，使得点N和M 被点R“关联”，请在图1 中画出符合条件的抛物线W2；
    （3）正方形EFGH的顶点分别是E（-4，1），F（-4，-1），G（-2，-1），H（-2，1），⊙T的圆心为T（3，0），半径为1．请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形（若涉及平面中某个区域时可以用阴影表示），并直接写出该图形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神，实施全国亿万学生每天集体锻炼一小时活动，吸引同学们走向操场、走进大自然、走到阳光下，积极参加体育锻炼，掀起校园内体育锻炼热潮，我市各学校结合实际情况举办了“阳光体育”系列活动，为了解“阳光体育”活动的落实情况，我市教育部门在红旗中学2000名学生中，随机抽取了若干名学生进行问卷调查（要求每位学生只能填写一种自己喜欢的活动），并将调查结果绘制成如下两幅不完整的统计图．

    根据以上信息，解答下列问题：
    （1）参加调查的人数共有300人，在扇形统计图中，表示“C”的扇形的圆心角为108度；
    （2）补全条形统计图，并计算扇形统计图中m的值；
    （3）若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练，则喜欢该项目的小丽同学被选中的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，点A、B为x轴上的两点，点C、D为y轴上的两点，经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线，我们把这条封闭曲线成为“月线”．已知点C的坐标为（0，3），点M是抛物线C2：y=mx2-4mx-12m（m＜0）的顶点．
    （1）求A、B两点的坐标；
    （2）在第一象限内的抛物线C1上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
    （3）连接AC、CM、DA，当AC∥DM时，证明：AD∥CM．

    查看答案和解析>>

    同步练习册答案