
分析 由菱形的性质得出AB=BC=CD=DA,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD,AC⊥BD,由菱形的面积求出BD,得出OB,根据勾股定理求出AB即可.
解答 解:如图所示: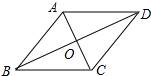 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD,AC⊥BD,
∴菱形的面积=$\frac{1}{2}$AC•BD=24,
∴BD=8,
∴OB=$\frac{1}{2}$BD=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
故答案为:5.
点评 本题考查了菱形的性质、菱形面积的计算以及勾股定理;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
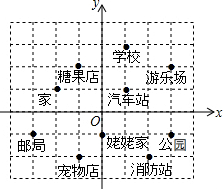 下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{20}$ | B. | $\sqrt{19}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{5}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com