练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在一张长为8cm，宽为6cm的矩形纸片上，现要剪下一个腰长为5cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上）．则剪下的等腰三角形的面积为______cm2．

    【答案】或5或10

    【解析】试题分析：因为等腰三角形腰的位置不明确，所以分（1）腰长在矩形相邻的两边上，（2）一腰在矩形的宽上，（3）一腰在矩形的长上，三种情况讨论．

    （1）△AEF为等腰直角三角形，直接利用面积公式求解即可；

    当AE=AF=5厘米时，∴S△AEF=AEAF=×5×5=厘米2；

    （2）当AE=EF=5厘米时，如图：

    先利用勾股定理求出AE边上的高BF=厘米，所以S△AEF=AEBF=×5×=厘米2；

    （3）当AE=EF=5厘米时，如图：

    先求出AE边上的高DF=4厘米，所以S△AEF=AEDF=×5×4=10厘米2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某班12位同学参加每周一次的教室卫生大扫除，有扫地、擦玻璃和擦课桌椅三个项目，扫地的面积为88 m2，擦玻璃的面积为32 m2，根据实际情况将三个项目的面积分配情况和每人每分钟完成各项目的工作量制作如下统计图：

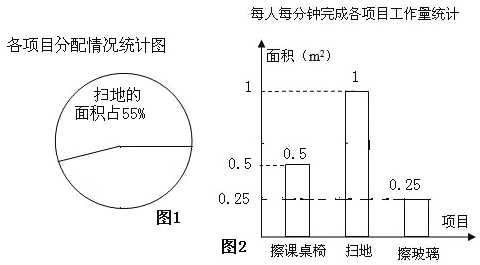
    (1)擦课桌椅的面积为__________，请补全图1中的各项目面积分配情况扇形统计图；

    (2)卫生委员设计两种方案：

    方案一：12位同学先一起完成扫地任务，再一起完成擦玻璃任务，最后一起完成擦课桌椅任务；

    方案二：12位同学先一起完成扫地任务后，再把这12位同学分成两组，每组6人，一组擦玻璃，一组去擦课桌椅.

    你认为这哪种方案完成大扫除任务所用的时间少，少多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

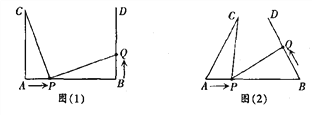
    【题目】如图(1)，AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t(s)．

    (1)若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；

    (2)如图(2)，将图(1)中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某人存入5000元参加三年期教育储蓄(免征利息税)，本息共得5417元，那么这种储蓄的年利率为

    A．2．22%B．2．58%C．2．78% D．2．38%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个城镇A、B与两条公路l1、l2位置如图所示，电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路l1，l2的距离也必须相等，那么点C应选在何处？请在图中，用尺规作图找出所有符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

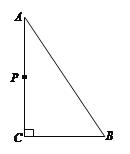
    【题目】如图，△ABC中，∠C=90°，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．

    （1）若点P恰好在∠BAC的角平分线上，求t的值；

    （2）问t为何值时，△BCP为等腰三角形？

    （3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）

    A.（3+x）（4-0．5x）=15B.（x+3）（4+0．5x）=15

    C.（x+4）（3-0．5x）=15D.（x+1）（4-0．5x）=15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=a（x﹣h）2+k（a＞0），其图象过点A（0，2），B（8，3），则h的值可以是（　　）
    A.6
    B.5
    C.4
    D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝x2﹣2在y轴右侧的部分是_____．（填“上升”或“下降”）

    查看答案和解析>>

    同步练习册答案