
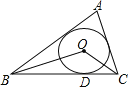
【题目】如图:△ABC的内切圆O与边BC切于点D,若∠BOC=135°,BD=3,CD=2,则△ABC的面积为=______.
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x-c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
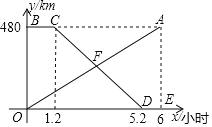
【题目】甲、乙两地相距480km,一辆货车从甲地匀速驶往乙地,货车出发一段时间后,一辆汽车从乙地匀速驶往甲地,设货车行驶的时间为![]() 线段OA表示货车离甲地的距离
线段OA表示货车离甲地的距离![]() 与xh的函数图象;折线BCDE表示汽车距离甲地的距离
与xh的函数图象;折线BCDE表示汽车距离甲地的距离![]() 与
与![]() 的函数图象.
的函数图象.
![]() 求线段OA与线段CD所表示的函数表达式;
求线段OA与线段CD所表示的函数表达式;
![]() 若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义;
若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义;
![]() 当x为何值时,两车相距100千米?
当x为何值时,两车相距100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地的火车原来的平均速度是100千米每小时,经过两次提速后平均速度为121千米每小时,这两次提速的百分率相同.
(1)求该火车每次提速的百分率;
(2)若甲乙两地铁路长220千米,求第一次提速后从甲地到乙地所用的时间比提速前少用了多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
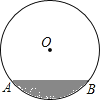
【题目】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
(1)若油面宽AB=16dm,求油的最大深度.
(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?
查看答案和解析>>
科目:初中数学 来源: 题型:
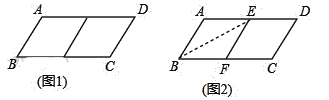
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:

(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
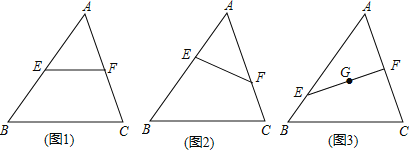
【题目】在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:![]()
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com