
【题目】张华发现某月的日历中一个有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
(1)此日历中能画出 个十字框?
(2)若a+b+c+d=84,求k的值;
(3)是否存在k的值,使得a+b+c+d=108,请说明理由.

【答案】(1)12;(2)k=21;(3)不存在k的值,使得a+b+c+d=108,理由见解析.
【解析】(1)直接利用已知图表分析得出符合题意的位置;
(2)利用日历中数据之间的关系进而得出k的值;
(3)利用日历中数据之间的关系进而分析得出答案.
(1)由题意可得:十字框顶端分别在:1,2,5,6,7,8,9,12,13,14,15,16一共有12个位置;
(2)由题意可得:设最上面为a,最左边为b,最右边为c,最下面为d,
则b=a+6,c=a+8,d=a+14,k=a+7,
故a+a+6+a+8+a+14=84,
解得:a=14,
则k=21;
(3)不存在k的值,使得a+b+c+d=108,
理由:当a+b+c+d=108,
则a+a+6+a+8+a+14=108,
解得:a=20,故d=34>31(不合题意),
故不存在k的值,使得a+b+c+d=108.


科目:初中数学 来源: 题型:
【题目】读图,回答问题
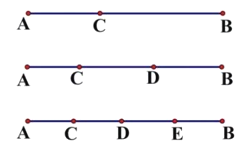
(1)在线段![]() 上取一点
上取一点![]() ,共有 条线段;
,共有 条线段;
(2)在线段![]() 上取两点
上取两点![]() ,共有 条线段;
,共有 条线段;
(3)在线段![]() 上取三点
上取三点![]() ,共有 条线段;
,共有 条线段;
(4)在线段![]() 上取
上取![]() 个点,共有 条线段.
个点,共有 条线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂家本周计划每天生产300辆摩托车,由于工厂实行轮休,每天上班人数不一定相等,实际每天生产与计划相比情况如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +7 | ﹣3 | +4 | +10 | ﹣9 | ﹣25 |
(1)本周六生产了多少辆摩托车?
(2)本周总产量与计划相比是增加了还是减少了?具体数量是多少?产量最多的一天比产量最少的一天多生产了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;

于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
![]()
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,一辆城管汽车在一条东西方向的公路上巡逻.如果规定向东为正,向西为负,从出发点开始它所行走的记录为(长度单位:千米):![]() .
.
(1)此时这辆城管汽车的司机应如何向队长描述他的位置?
(2)如果队长命令他马上返回出发点,那么这次巡逻(含返回)共耗油多少升(已知每千米耗油![]() 升)?
升)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)(﹣2x)3x6÷(﹣3x3)2
(2)5m(m﹣n)﹣(5m+n)(m﹣n)
(3)利用简便方法计算:20202﹣2019×2021
(4)先化简,再求值:[(a+b)2﹣(a﹣b)(a+b)]÷(2b),其中a=﹣![]() ,b=﹣1.
,b=﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:![]() =
=![]() ;
;
(3)若AO=2![]() ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.
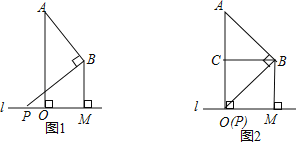
查看答案和解析>>
科目:初中数学 来源: 题型:
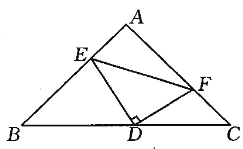
【题目】如图,在等腰直角△ABC中,AB=AC,点D是斜边BC的中点,点E、F分别是AB、AC边上的点,且DE⊥DF.
(1)证明:BE+CF=EF2;
(2)若BE=12,CF=5,求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com