
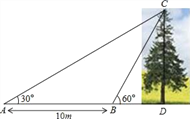
����Ŀ����ͼ��ij��ѧ��ȤС�������һ����CD�ĸ߶ȣ��������ڵ�A���������C������Ϊ30�㣬Ȼ����AD����ǰ��10m������B�㣬��B���������C�����Ǹ߶�Ϊ60�㣨A��B��D������ͬһֱ���ϣ�������������Dz������ݼ��������CD�ĸ߶ȣ������ȷ��0.1m�������ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
���𰸡�8.7��
������������������������������ε���ǵ����������ACB�Ķ������õ�BC�ij��ȣ�Ȼ����ֱ����BDC�У��������Ǻ���������⣮
����������ߡ�CBD=��A+��ACB��
���ACB=��CBD����A=60�㩁30��=30����
���A=��ACB��
��BC=AB=10���ף���
��ֱ����BCD�У�CD=BCsin��CBD=10��![]() =5
=5![]() ��5��1.732=8.7���ף���
��5��1.732=8.7���ף���
�������CD�ĸ߶�Ϊ8.7�ף�
���㣺��ֱ�������ε�Ӧ��
�����͡������
��������
23
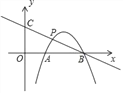
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��x2+ax+b��x����A��1��0����B��3��0�����㣬��P�����������ڵ�һ�����ڵ�һ�㣬ֱ��BP��y���ཻ�ڵ�C��
��1����������y=��x2+ax+b�Ľ���ʽ��
��2������P���߶�BC���е�ʱ�����P�����ꣻ
��3���ڣ�2���������£���sin��OCB��ֵ��
���𰸡�(1) y=��x2+4x��3��(2) ��P������Ϊ��![]() ��
��![]() ����(3)
����(3) ![]() .
.
����������������1������A��B����������y=-x2+ax+b�����a��b�ɵý���ʽ��
��2����C�������Ϊ0�ɵ�P������꣬��P���������루1���������߽���ʽ����P�����ꣻ
��3����P�������ɵ�C�����꣬A��B��C�����꣬���ù��ɶ����ɵ�BC��������sin��OCB=![]() �ɵý����
�ɵý����
��⣺��1������A��B����������y=��x2+ax+b�ɵã�
![]() ��
��
��ã�a=4��b=��3��
�������ߵĽ���ʽΪ��y=��x2+4x��3��
��2���ߵ�C��y���ϣ�
����C�������x=0��
�ߵ�P���߶�BC���е㣬
���P������xP=![]() =
=![]() ��
��
�ߵ�P��������y=��x2+4x��3�ϣ�
��yP=![]()
![]() ��3=
��3=![]() ��
��
���P��������![]() ��
��![]() ����
����
��3���ߵ�P������Ϊ��![]() ��
��![]() ������P���߶�BC���е㣬
������P���߶�BC���е㣬
���C��������Ϊ2��![]() ��0=
��0=![]() ��
��
���C��������0��![]() ����
����
��BC=![]() =
=![]() ��
��
��sin��OCB=![]() =
=![]() =
=![]() ��
��


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮ�˴������������ǿ����������������г���������ɡ�ƽ�ȡ����������Σ�������������ҵ�����š����ƣ����������ͼ������������ļ�ֵ������24���������������ļ�ֵ�۵Ļ������������У�
����ǿ����������������г������������ļ�ֵĿ����
�����ɡ�ƽ�ȡ����������������������ļ�ֵȡ����
����������ҵ�����š��������������������ļ�ֵ����

С��ͬѧ�����е���������������г����������������ƽ���������ֱַ�����4��Ӳֽ���ϣ��Ƴ�����ͼ��ʾ�Ŀ�Ƭ������4�ſ�Ƭ���泯��ϴ�Ⱥ���������ϣ����������ȡһ�ſ�Ƭ�����Ż����������ȡһ�ſ�Ƭ��
��1��С���һ�γ�ȡ�Ŀ�Ƭ�ϵ����������������ֵĿ��ĸ����� ��
��2���������б�������״ͼ��������С��������γ�ȡ��Ƭ�ϵ�����һ�������������ֵĿ�ꡢһ��
����������ֵȡ��ĸ�������Ƭ���ƿ�����ĸ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪֱ��AB��һ�㣬��COE��90�� ��OF ƽ�֡�AOE��
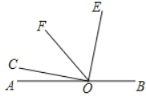
��1������BOE��80�������COF�Ķ�����
��2������COF����(0��������90��)�����BOE�� (�ú�����ʽ�ӱ�ʾ) ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
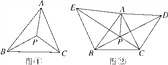
����Ŀ����ͼ����PΪ��ABC����ƽ����һ�㣬�ҡ�APB����BPC����CPA��120�������P������ABC�ķ����㣮
(1)�����PΪ��ǡ�ABC�ķ����㣬�ҡ�ABC��60��.
����֤�� ��ABP�ס�BCP��
����PA��3��PC��4����PB�ij���
(2)��ͼ�ڣ���֪��ǡ�ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD�ཻ�ڵ�P������AP.
�����CPD�Ķ�����
����֤����PΪ��ABC�ķ����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н���:��ƽ����3��ֱ�������ཻ������3������;����ƽ���ڣ�����AOB =40������AOC= ��BOC,���AOC�Ķ���Ϊ20��;�����߶�AB=3, BC=2�����߶�AC�ij�Ϊ1��5;������a+����=180�����ҡ�a<���������a�����Ϊ![]() (����-��a).������ȷ���۵ĸ����� ��
(����-��a).������ȷ���۵ĸ����� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н��ۣ��ټ�����������ˣ������и������������������Ϊ�������������ζ���ʽ�ĺ�һ�������ζ���ʽ������xyz��0����![]() +
+![]() +
+![]() +
+![]() ��ֵΪ0��4������a��b��Ϊ�෴������
��ֵΪ0��4������a��b��Ϊ�෴������![]() ����1������x��y����
����1������x��y����![]() ��
��![]() ��������ȷ�ĸ����У�������
��������ȷ�ĸ����У�������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
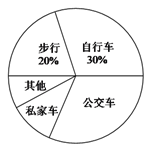
����Ŀ��ijУΪ�˽�ȫУ2400��ѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飮�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ��ֻ��ѡһ��Ҳ��ܲ�ѡ��������õ��Ľ�����Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������������
��1����ε����У�һ����ȡ�˶�����ѧ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3������ȫУ����ѧ�����ж����˳�����������ѧ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��������ͬʱ�����330ǧ�ļס�������������У�s��ǧ�ף���ʾ������صľ��룬t���֣���ʾ������ʻ��ʱ�䣬��ͼ��L1��L2�ֱ��ʾ����������s��t�Ĺ�ϵ��
��1��L1��ʾ�����������صľ�������ʻʱ��Ĺ�ϵ��
��2������B���ٶ��Ƕ��٣�
��3����L1��L2�ֱ��ʾ������������s��t�Ĺ�ϵʽ��
��4��2Сʱ������������ǧ�ף�
��5����ʻ�ʱ���A��B����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���о����κ���![]() ��
��![]() Ϊ����������ʱ�����½��ۣ��ٸö��κ���ͼ��Ķ���ʼ����ƽ����x���ֱ���ϣ��ڸö��κ���ͼ��Ķ�����x����������㹹�ɵ���ֱ�������Σ��۵�
Ϊ����������ʱ�����½��ۣ��ٸö��κ���ͼ��Ķ���ʼ����ƽ����x���ֱ���ϣ��ڸö��κ���ͼ��Ķ�����x����������㹹�ɵ���ֱ�������Σ��۵�![]() ʱ��y��x�������������m��ȡֵ��ΧΪ
ʱ��y��x�������������m��ȡֵ��ΧΪ![]() ���ܵ�
���ܵ�![]() ���
���![]() �ں���ͼ���ϣ���
�ں���ͼ���ϣ���![]() ��
��![]() ����
����![]() .������ȷ���۵ĸ���Ϊ�� ��
.������ȷ���۵ĸ���Ϊ�� ��
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com