
【题目】若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形__________“奇妙四边形”(填“是”或“不是”);
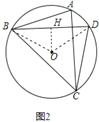
(2)如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;
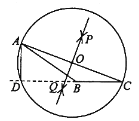
(3)如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”,作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.

【答案】1)不是;(2)54;(3)OM=![]() AD.理由见解析.
AD.理由见解析.
【解析】试题分析:(1)根据矩形的性质和“奇妙四边形”的定义进行判断;
(2)连结OB、OD,作OH⊥BD于H,如图2,根据垂径定理得到BH=DH,根据圆周角定理得到∠BOD=2∠BCD=120°,则利用等腰三角形的性质得∠OBD=30°,在Rt△OBH中可计算出BH=![]() OH=3
OH=3![]() ,BD=2BH=6
,BD=2BH=6![]() ,则AC=BD=6
,则AC=BD=6![]() ,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
(3)连结OB、OC、OA、OD,作OE⊥AD于E,如图3,根据垂径定理得到AE=DE,再利用圆周角定理得到∠BOM=∠BAC,∠AOE=∠ABD,再利用等角的余角相等得到∠OBM=∠AOE,则可证明△BOM≌△OAE得到OM=AE,于是有OM=![]() AD.
AD.
试题解析:(1)矩形的对角线相等但不垂直,
所以矩形不是“奇妙四边形”,
故答案为:不是;
(2)连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,∴OH=![]() OB=3,∴BH=
OB=3,∴BH=![]() OH=3
OH=3![]() ,
,
∵BD=2BH=6![]() ,∴AC=BD=6
,∴AC=BD=6![]() ,
,
∴“奇妙四边形”ABCD的面积=![]() ×6
×6![]() ×6
×6![]() =54;
=54;
(3)OM=![]() AD.理由如下:
AD.理由如下:
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,∴AE=DE,
∵∠BOC=2∠BAC,而∠BOC=2∠BOM,∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,∴∠BAC+∠ABD=90°,∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,∴∠OBM=∠AOE,
在△BOM和△OAE中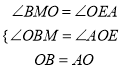 ,
,
∴△BOM≌△OAE,∴OM=AE,∴OM=![]() AD.
AD.


科目:初中数学 来源: 题型:
【题目】甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有![]() 个白球、
个白球、![]() 个蓝球;乙盒中有
个蓝球;乙盒中有![]() 个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的
个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的![]() 倍.
倍.
(![]() )求乙盒中蓝球的个数.
)求乙盒中蓝球的个数.
(![]() )从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(-4,0),B(2,6)两点.
(1)求一次函数y=kx+b的表达式;
(2)在直角坐标系中,画出这个函数的图象;
(3)求这个一次函数与坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知: ![]() .
.

求作: ![]() 边上的高
边上的高![]()
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
, ![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心, ![]() 为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
请回答;该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮用如下(图4)的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对
双方公平吗?请说明理由;若不公平,请你修改规则使游戏对双方公平.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com