
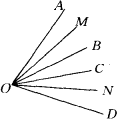
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB、ON平分∠COD,若∠AOD=α,∠MON=β求∠BOC的大小(用含α、β的式子表示).
|
解:因为OM平分∠AOB,ON平分∠COD, 所以∠AOB=2∠AOM,∠COD=2∠DON. 又因为∠BOC=∠AOD-(∠AOB+∠COD), 故有∠BOC=∠AOD-2(∠AOM+∠DON), 又∠AOM+∠DON=∠AOD-∠MON. 所以∠BOC=∠AOD-2(∠AOD-∠MON). 所以∠BOC=2∠MON-∠AOD. 即∠BOC=2β-α 精析:求∠BOC的大小,要找出∠BOC与∠AOD、∠MON的关系,∠BOC=∠AOD-(∠AOB+∠COD)=∠AOD-2(∠AOM+∠DON)=∠AOD-2(∠AOD-∠MON). |
|
根据题意,观察图形找到∠BOC与∠AOD、∠MON的关系,再利用角的和差及角平分线的关系解答. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
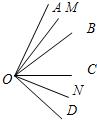 26、如图:已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,
26、如图:已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
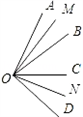
 如图:已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,
如图:已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,查看答案和解析>>
科目:初中数学 来源:河北省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com