
【题目】若m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( )=0,
即( )2+( )2=0.根据非负数的性质,
∴m=n=
完善上述解答过程,然后解答下面的问题:
设等腰三角形ABC的三边长a、b、c,且满足a2+b2-4a-6b+13=0,求△ABC的周长.
【答案】8
【解析】
先根据“添括号法则”结合“完全平方公式”将例题的解答过程补充完整,然后参考例题的解题方法,将等式a2+b2-4a-6b+13=0变形为![]() ,进而化为
,进而化为![]() 即可得到
即可得到![]() ,这样再结合△ABC是等腰三角形即可求出△ABC的周长了.
,这样再结合△ABC是等腰三角形即可求出△ABC的周长了.
(1)完善例题的解题过程:
∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( n2-8n+16 )=0,
即( m-n )2+( n-4 )2=0,
∴m=n= 4 ;
(2)∵a2+b2-4a-6b+13=0,
∴![]() ,
,
∴![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,
,
∵等腰△ABC的三边长为:a、b、c,
∴当![]() 时,三边分别为:2、2、3,此时能围成三角形,△ABC的周长=2+2+3=7;
时,三边分别为:2、2、3,此时能围成三角形,△ABC的周长=2+2+3=7;
当![]() 时,三边分别为:2、3、3,此时能围成三角形,△ABC的周长=2+3+3=8;
时,三边分别为:2、3、3,此时能围成三角形,△ABC的周长=2+3+3=8;
综上所述,等腰△ABC的周长为7或8.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.

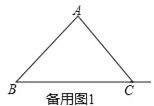

(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请求出DE的长.
,当CD=1时,请求出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
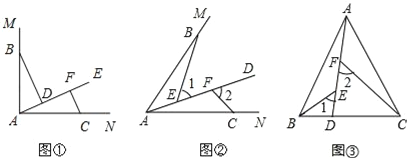
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司仓库本周内货物进出的吨数记录如下![]() “
“![]() ”表示进库,“
”表示进库,“![]() ”表示出库
”表示出库![]() ;
;
日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
吨数 |
|
|
|
|
|
|
|
![]() 这一周,仓库内货物的总吨数是______了
这一周,仓库内货物的总吨数是______了![]() 填“增多”或“减少”
填“增多”或“减少”![]() ;
;
若周六结束时仓库内还有货物360吨,则周日开始时仓库内有货物多少吨?
![]() 如果该仓库货物进出的装卸费都是每吨5元,那么这一周内共需付多少元的装卸费?
如果该仓库货物进出的装卸费都是每吨5元,那么这一周内共需付多少元的装卸费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com