
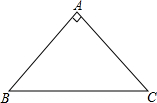
 知图,△ABC中,AB=AC,∠A=90°.
知图,△ABC中,AB=AC,∠A=90°.分析 (1)首先以B为圆心,任意长为半径画弧,交AB、BC与M、N,再以M、N为圆心,大于$\frac{1}{2}$MN长为半径画弧,两弧交于点K,再画射线BK交AC于D,BD就是△ABC的角平分线BD;
(2)过D作DE⊥BC于E,根据角平分线性质求出AD=DE,推出AB=BE,求出∠C=∠EDC,推出AD=DE=CE,代入求出即可.
解答 
 解:(1)如图所示:
解:(1)如图所示:
(2).证明:过D作DE⊥BC于E,
∵BD平分∠ABC,DE⊥BC,∠DAB=90°,
∴AD=DE,
由勾股定理得:AB2=BD2-AD2,BE2=BD2-DE2,
∴AB=BE,
∵∠A=90°,AC=AB,
∴∠C=∠ABC=$\frac{1}{2}$(180°-90°)=45°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠EDC=180°-90°-45°=45°=∠C,
∴DE=EC,
∴BC=BE+CE=AB+AD.
点评 此题主要考查了基本作图,以及角平分线的性质,关键是正确画出图形,掌握角的平分线上的点到角的两边的距离相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
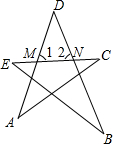 如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?
如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com