
 如图,在菱形ABCD的边BC的延长线上作等边△CEF中,∠ABC=120°,H是AE的中点,连接DF、DH、FH.
如图,在菱形ABCD的边BC的延长线上作等边△CEF中,∠ABC=120°,H是AE的中点,连接DF、DH、FH.分析 (1)先判断出△AHG≌△EHF,得出HG=HF,AG=EF,再判断出△ADG≌△CDF,得出DG=DF,即可;
(2)先判断出四边形BEFG是平行四边形,求出GF=3,再用(1)得出的结论HG=HF即可.
解答 解:(1)如图,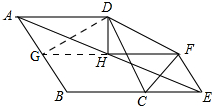
∵四边形ABCD是菱形,
∴AB∥DC,∠BCD=60°,
∵△CEF是等边三角形,
∴∠CFE=∠ECF=60°,
∴∠DCF=60°,
∴∠CFE=∠DCF,
∴EF∥DC∥AB,
∴∠GAH=∠FEH,∠AGH=∠EFH,
∵H是AE的中点,
∴AH=EH
在△AHG和△EHF中$\left\{\begin{array}{l}{∠AGH=∠EFH}\\{∠GAH=∠FEH}\\{AH=EH}\end{array}\right.$,
∴△AHG≌△EHF,
∴HG=HF,AG=FE,
∵△CEF是等边三角形,
∴CF=FE,
∴AG=CF,
∵四边形ABCD是菱形,
∴AD=CD,∠GAD=60°,
∴∠GAD=∠FCD,
在△ADG和△DCF中
∵$\left\{\begin{array}{l}{AG=FC}\\{∠GAD=∠FCD}\\{AD=CD}\end{array}\right.$,
∴△ADG≌△DCF,
∴DG=DF,
∵HG=HF,
∴DH⊥HF,
(2)由(1)知,AG=EF,
∵AB=2,AG=EF=EC=1,
∴BG=AB-AG=1,
∴BG=EF,
由(1)知,AB∥EF,
∴四边形BEFG是平行四边形,
∴FG=BE=BC+CE=AB+CE=3,
由(1)知HG=HF,
∴HF=$\frac{1}{2}$GF=$\frac{3}{2}$.
点评 本题是菱形的性质,主要考查了全等三角形的性质和判定,菱形的性质,等腰三角形的性质和判定的应用,解本题的关键是判断出△ADG≌△CDF,


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2016-2017学年山东省淄博市(五四学制)六年级下学期第一次月考数学试卷(解析版) 题型:单选题
如果□×3(ab)2=9a3b2,则□内应填的代数式是( )
A. ab B. 3ab C. a D. 3a
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,AF,BG,CH,DE依次交于点M,N,P,Q,连接PM,QN,求证:PM与QN互相平分.
如图,在?ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,AF,BG,CH,DE依次交于点M,N,P,Q,连接PM,QN,求证:PM与QN互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,E是BC上一点,DE、AB的延长线交于点F,且AB=BF,DE=EF,S△SBE=S△DEF,求证:四边形ABCD为平行四边形.
如图,在四边形ABCD中,E是BC上一点,DE、AB的延长线交于点F,且AB=BF,DE=EF,S△SBE=S△DEF,求证:四边形ABCD为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的顶点都在方格线的交点(格点)上
如图,△ABC的顶点都在方格线的交点(格点)上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.
如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 精确到百位,有2个有效数字 | B. | 精确到十分位,有2个有效数字 | ||
| C. | 精确到千分位,有2个有效数字 | D. | 精确到万分位,有2个有效数字 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | |
| B. | 两直线平行,内错角相等 | |
| C. | 点到直线的距离是该点到这条直线的垂线段的长度 | |
| D. | 同角或等角的余角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com