
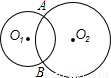
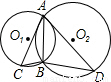
 解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,
解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,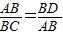 ,
,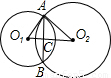
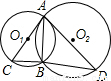
 根据切割线定理,得DA2=DB•DC;
根据切割线定理,得DA2=DB•DC;

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
 如图;⊙Ol、⊙O2相交于点A、B,现给出4个命题:
如图;⊙Ol、⊙O2相交于点A、B,现给出4个命题:查看答案和解析>>
科目:初中数学 来源: 题型:
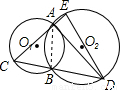
 11、如图,⊙Ol和⊙O2外切于A,PA是内公切线,BC是外公切线,B、C是切点.①PB=AB;②∠PBA=∠PAB;③△PAB∽△OlAB;④PB•PC=OlA•O2A.上述结论,正确结论的个数是(B )
11、如图,⊙Ol和⊙O2外切于A,PA是内公切线,BC是外公切线,B、C是切点.①PB=AB;②∠PBA=∠PAB;③△PAB∽△OlAB;④PB•PC=OlA•O2A.上述结论,正确结论的个数是(B )查看答案和解析>>
科目:初中数学 来源: 题型:
 13、如图,⊙Ol和⊙O2内切于点P,⊙O2的弦AB经过⊙Ol的圆心Ol,交⊙Ol于C、D,若AC:CD:DB=3:4:2,则⊙Ol与⊙O2的直径之比为( )
13、如图,⊙Ol和⊙O2内切于点P,⊙O2的弦AB经过⊙Ol的圆心Ol,交⊙Ol于C、D,若AC:CD:DB=3:4:2,则⊙Ol与⊙O2的直径之比为( )查看答案和解析>>
科目:初中数学 来源: 题型:
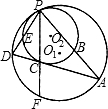 如图,⊙Ol和⊙O2内切于点P,过点P的直线交⊙Ol于点D,交⊙O2于点E,DA与⊙O2相切,切点为C.
如图,⊙Ol和⊙O2内切于点P,过点P的直线交⊙Ol于点D,交⊙O2于点E,DA与⊙O2相切,切点为C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com