
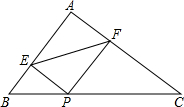
 如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8.
如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为4.8. 分析 先利用勾股定理的逆定理证明△ABC为直角三角形,∠A=90°,则证明四边形AEPF为矩形,连接AP,如图,则EF=AP,当AP的值最小时,EF的值最小,利用垂线段最短得到AP⊥BC时,AP的值最,然后利用面积法计算此时AP的长即可.
解答 解:∵AB=6cm,AC=8cm,BC=10cm,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,∠A=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴∠AEP=∠AFP=90°,
∴四边形AEPF为矩形,
连接AP,如图,EF=AP,当AP的值最小时,EF的值最小,
当AP⊥BC时,AP的值最,此时AP=$\frac{6×8}{10}$=$\frac{24}{5}$,
∴EF的最小值为$\frac{24}{5}$.
故答案为4.8.
点评 此题考查了矩形的判定与性质:关于矩形,应从平行四边形的内角的变化上认识其特殊性:一个内角是直角的平行四边形,进一步研究其特有的性质:是轴对称图形、内角都是直角、对角线相等.同时平行四边形的性质矩形也都具有.在处理许多几何问题中,若能灵活运用矩形的这些性质,则可以简捷地解决与角、线段等有关的问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+0.5)(a-0.5) | B. | (x+y)(-x-y) | C. | (3a+4b)(3b-4a) | D. | (a2+b2)(a2+b2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
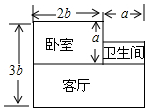 小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖
小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖查看答案和解析>>
科目:初中数学 来源: 题型:解答题
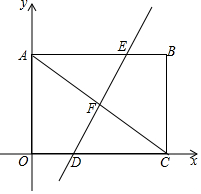 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com