
分析 由|2x-3y|≥0即当2x=3y时,知|2x-3y|取得最小值0;根据|2x-3y|=$\sqrt{(2x-3y)^{2}}$=$\sqrt{4{x}^{2}+9{y}^{2}-12xy}$知当12xy为最小值0时,|2x-3y|=$\sqrt{4{x}^{2}+9{y}^{2}-12xy}$取得最大值,分别求出x=0或y=0时的值即可得答案.
解答 解:∵|2x-3y|≥0 即当2x=3y时,|2x-3y|取得最小值为0;
由3x+4y≤12知:0≤x≤4 0≤y≤3,
∵|2x-3y|=$\sqrt{(2x-3y)^{2}}$=$\sqrt{4{x}^{2}+9{y}^{2}-12xy}$,
∴当12xy为最小值0时,|2x-3y|=$\sqrt{4{x}^{2}+9{y}^{2}-12xy}$取得最大值,
即x与y中至少有一个数为0,另一个取最大值,
当x=0时,|2x-3y|=9,
当y=0时,|2x-3y|=8,
综上所述:|2x-3y|的最大值为9,最小值为0.
点评 本题主要考查绝对值,熟练掌握绝对值的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 图中的容量器是两个形状、大小相同、高度相等都为Hdm的圆台形容器构成,若往此容器中注水,设注入容器中水的高度为h(dm),注水时间为t(s),则h关于t的函数图象是( )
图中的容量器是两个形状、大小相同、高度相等都为Hdm的圆台形容器构成,若往此容器中注水,设注入容器中水的高度为h(dm),注水时间为t(s),则h关于t的函数图象是( )| A. | 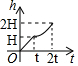 | B. | 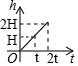 | C. | 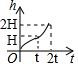 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②④ | C. | ①②⑤ | D. | ①②④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com