
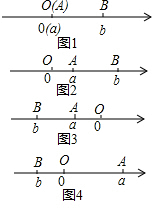
 (1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,
(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|,当A、B两点都不在原点时,分析 ①根据两点间距离公式计算即可.
②根据两点间距离公式计算,把问题转化为方程解决.
③当x≤-3时,无解.当-3<x<5时,1<x<5,当x≥5时,不等式恒成立,由此即可解决问题.
④求代数式|x+2|+|x-3|+|x-1|的最小值就是在数轴上找一点P到表示-2,1,3的点的距离之和最小,当P与表示1的点重合时,点P到表示-2,1,3的点的距离之和最小.
解答 解:①数轴上表示1005和-1011的两点之间的距离是|1005-(-1011)|=2016,
故答案为:2016;
②数轴上分别表示x、-5的两点A、B之间的距离是|x+5|,
∵|AB|=2,
∴|x+5|=2,
解得:x=-3或-7,
故答案为:|x+5|,-3或-7;
③|x+3|>|x-5|,则相应x的取值范围是:
当x≤-3时,无解.
当-3<x<5时,1<x<5,
当x≥5时,不等式恒成立,
综上所述,x的取值范围为x>1.
故答案为x>1.
④代数式|x+2|+|x-3|+|x-1|的最小值为,
求代数式|x+2|+|x-3|+|x-1|的最小值就是在数轴上找一点P到表示-2,1,3的点的距离之和最小,当P与表示1的点重合时,点P到表示-2,1,3的点的距离之和最小,最小值为5.
故答案为5.
点评 本题考查实数与数轴、绝对值.两点间距离公式等知识,解题的关键是理解题意,把问题转化为方程解决,学会用绝对值的几何意义解决实际问题,属于中考常考题型.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com