
 已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:
已知:某大型水果种植中心对去年某种时令水果的销售情况统计如下:上半年的销售单价y1(元/千克)与月份x(月)(1≤x≤6,且x为整数)的关系.如下表所示:| x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| y1(元/千克) | 36 | 18 | 12 | 9 | 7.2 | 6 |
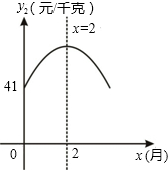
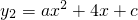 ,其图象如图所示.同时,去年上半年的销售量为z1(万千克)与月份x(月)(1≤x≤6,且x为整数)的函数关系式为
,其图象如图所示.同时,去年上半年的销售量为z1(万千克)与月份x(月)(1≤x≤6,且x为整数)的函数关系式为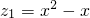 ;去年下半年的销量一直稳定在每月10万千克.
;去年下半年的销量一直稳定在每月10万千克. )
) 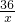 ,
,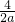 =2,
=2,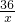 •(x2-x)=36x-36,
•(x2-x)=36x-36,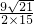 =
=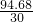 ,
,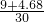 =0.456或a%=
=0.456或a%=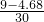 =0.144,
=0.144,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com