

分析 记原来三角形的面积为s,第一个小三角形的面积为s1,第二个小三角形的面积为s2,…,求出s1,s2,s3,探究规律后即可解决问题.
解答 解:记原来三角形的面积为s,第一个小三角形的面积为s1,第二个小三角形的面积为s2,…,
∵s1=$\frac{1}{4}$•s=$\frac{1}{{2}^{2}}$•s,
s2=$\frac{1}{4}$•$\frac{1}{4}$s=$\frac{1}{{2}^{4}}$•s,
s3=$\frac{1}{{2}^{6}}$•s,
∴sn=$\frac{1}{{2}^{2n}}$•s=$\frac{1}{{2}^{2n}}$•$\frac{1}{2}$•2•2=$\frac{1}{{2}^{2n-1}}$,
故答案为$\frac{1}{{2}^{2n-1}}$.
点评 本题考查三角形的中位线定理,三角形的面积等知识,解题的关键是循环从特殊到一般的探究方法,寻找规律,利用规律即可解决问题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
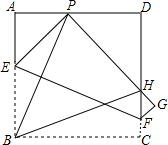 如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.
如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
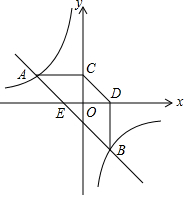 如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.
如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
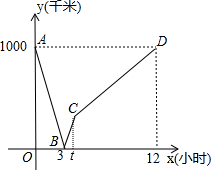 首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
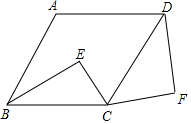 如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.
如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com