练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
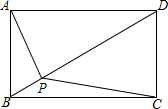
    8．已知：如图，在矩形ABCD内有一点P．求证：PA2+PC2=PB2+PD2．

    分析 首先过点P作EF∥AB，作MN∥BC，把矩形ABCD分成四个小矩形，然后分别表示出PA、PB、PC、PD的平方，根据平方关系即可得解．

    解答 证明：过点P作EF∥AB，作MN∥BC，
    则四边形AMPE，四边形BFPM，四边形FCNP，四边形NDEP都是矩形，
    根据勾股定理得，PA2=AE2+PE2，
    PB2=BF2+PF2，
    PC2=FC2+PF2，
    PD2=DE2+PE2，
    ∵AE=BF，DE=FC，
    ∴（AE2+PE2）+（FC2+PF2）=（BF2+PF2）+（DE2+PE2），
    即PA2+PC2=PB2+PD2．

    点评 此题考查了矩形的性质与判定以及勾股定理的应用．注意准确作出辅助线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．若点P（$\sqrt{5}$，a）在正比例函数y=-5x的图象上，则a=-5$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知实数x，y满足y=$\sqrt{2x-1}$-$\sqrt{1-2x}$+2，求$\sqrt{4x+5y-3}$的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在△ABC中，E是AB上一点，D是AC上一点，AE=6，AC=15，AD=8，AB=20，求证：△AED∽△ACB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知△ABC是锐角三角形，且sinA=0.7，求cosA，tanA的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．学习了有理数的运算后，王老师给同学们出了这样一道题：
    计算：71$\frac{15}{16}$×（-8），看谁算得又对又快．
    下面是两名同学给出的不同解法：
    小强：原式=-$\frac{1151}{16}$×8=-$\frac{1151}{2}$=-575$\frac{1}{2}$．
    小丽：原式=（71+$\frac{15}{16}$）×（-8）=71×（-8）+$\frac{15}{16}$×（-8）=-575$\frac{1}{2}$．
    （1）对以上两种解法，你认为谁的解法比较简便？
    （2）你还有其他解法吗？如果有，那么请写出解答过程．
    （3）你能用简便方法计算-99×$\frac{98}{99}$×198吗？如果能，那么请写出简答过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图所示，已知在△ABC中，∠C=90°，AD=AC，DE⊥AB交BC于点E，若∠B=28°，则∠EAC等于多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\root{3}{-27}$-$\sqrt{9}$+（$\sqrt{2}$）2；
    （2）|1-$\sqrt{2}$|-（$\sqrt{2}$+1）
    （3）$\sqrt{（1-\frac{5}{4}）^{2}}$+$\root{3}{\frac{7}{8}-1}$；
    （4）2$\sqrt{3}$-3$\sqrt{2}$+$\sqrt{5}$．（精确到0.01）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算24×（$\frac{1}{3}$-$\frac{5}{6}$-$\frac{7}{12}$+$\frac{11}{24}$）．

    查看答案和解析>>

    同步练习册答案