
 电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )
电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 首先根据题意,分别计算电子跳蚤的位置和三角形的顶点的距离,找到循环的规律:经过6次跳,电子跳蚤回到起跳点.根据这一规律确定第2015次落点的位置,从而确定点P2015与A间的距离.
解答 解:因为BP0=4,根据题意,CP0=10-4=6,
第一步从P0到P1,CP1=CP0=6;AP1=9-6=3,
第二步从P1到P2,AP2=AP1=3;BP2=8-3=5,
第三步从P2到P3,BP3=BP2=5;CP3=10-5=5,
第四步从P3到P4,CP4=CP3=5;AP4=9-5=4,
第五步从P4到P5,AP5=AP4=4;BP5=8-4=4,
第六步从P5到P6,BP6=BP5=4;
由此可知,P6点与P0点重合,又因为2015=6×335+5,所以P2015点与P5点重合,则点P2015与A点之间的距离为AP5=4.
故选B.
点评 本题考查规律型中的图形变化问题,解答该题主要是能够根据题意正确计算出有关线段的长,发现电子跳蚤的落点的循环规律,从而完成计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{7}$+$\sqrt{3}$=$\sqrt{10}$ | C. | $\sqrt{{x}^{2}}$=|x| | D. | ($\sqrt{-x}$)2=x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
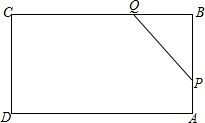 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )| A. | S=t2-6t+72 | B. | S=t2+6t+72 | C. | S=t2-6t-72 | D. | S=t2+6t-72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com