
【题目】如图所示,在平面直角坐标系中,等腰Rt△OAB的一条直角边OA 在x轴的正半轴上,点B在双曲线![]() 上,且∠BAO=90°,
上,且∠BAO=90°,![]() .
.
(1)求k的值及点A的坐标;
(2)△OAB沿直线OB平移,当点A恰好在双曲线上时,求平移后点A的对应点A′的坐标.

【答案】(1)k=4,A(2,0);(2) 点A坐标为![]() 或
或![]()
【解析】
(1)根据反比例函数系数k的几何意义即可求出k的值;根据△AOB的面积可求出OA的长,从而求出点A的坐标;
(2)过点A作直线 l∥OB,当△OAB沿直线OB移动时, 点A在直线l上移动.求出直线l的解析式,与反比例函数解析式组成方程组求解即可.
(1)∵![]() ,点B在双曲线上,
,点B在双曲线上,
∴![]() .
.
∵△OAB是等腰直角三角形,且∠BAO=90°,
∴![]() .
.
∴![]() .
.
∴A(2,0).
(2)过点A作直线 l∥OB,当△OAB沿直线OB移动时, 点A在直线l上移动.

∴当点A恰好在双曲线![]() 上时,
上时,
点A移动后的位置即为直线l与双曲线![]() 的交点.
的交点.
设![]() ,由点B(2,2)得
,由点B(2,2)得
2=2![]() ,解得
,解得![]() =1.
=1.
∴设直线l:y=x+b,由点A(2,0)得
0=2+b,解得b=-2.
∴y=x-2.
解方程组 得
得![]() 或
或![]() .
.
∴平移后的点A坐标为![]() 或
或![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象过点A(1,3),请根据下列条件试用无刻度的直尺分别在图1和图2中按要求画图.
的图象过点A(1,3),请根据下列条件试用无刻度的直尺分别在图1和图2中按要求画图.
(1)在图1中取一点B,使其坐标为(﹣1,﹣3);
(2)在图2中,在(1)中画图的基础上,画一个平行四边形ACBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
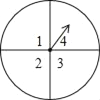
【题目】如图,把一个转盘分成四等份,依次标上数字1、2、3、4,若连续自由转动转盘二次,指针指向的数字分别记作a、b,把a、b作为点A的横、纵坐标.
(1)求点A(a,b)的个数;
(2)求点A(a,b)在函数y=x的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载了这样一个问题,大意为:有一个善于走路的人和一个不善于走路的人.善于走路的人走100步的同时,不善于走路的人只能走60步.现不善于走路的人先走100步,善于走路的人追他,则要走多少步才能追上(两人步长相等)?设善于走路的人走x步可追上,则可列方程为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
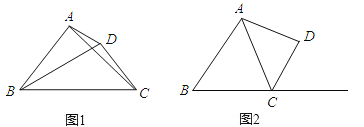
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
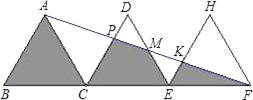
【题目】如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④S阴影=
CE;④S阴影=![]() .其中正确的个数为( )
.其中正确的个数为( )
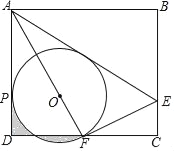
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com