
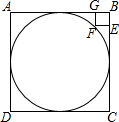
 圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )
圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )A、4+2
| ||
| B、2π | ||
C、5
| ||
D、
| ||
E、4
|
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
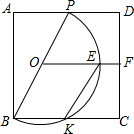 如图,正方形ABCD的边长为4,点P为线段AD上的一动点,(不与点A、D重合),以BP为直径在BP的右侧作半圆O,与边BC交于点K,边点O作OF∥AD,且与CD相交于点F,与半圆O相交于点E,连接KE,设AP=x,半圆O的面积为S,
如图,正方形ABCD的边长为4,点P为线段AD上的一动点,(不与点A、D重合),以BP为直径在BP的右侧作半圆O,与边BC交于点K,边点O作OF∥AD,且与CD相交于点F,与半圆O相交于点E,连接KE,设AP=x,半圆O的面积为S,查看答案和解析>>
科目:初中数学 来源: 题型:
 我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
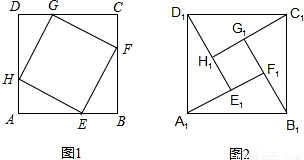 在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于
在正方形ABCD中,AB=4cm,点E,F,G,H分别是正方形的四条边上的点,且AE=BF=CG=DH.如图1所示.若把图1中的四个直角三角形剪下来,拼成如图2所示的面积为10cm2的正方形A1B1C1D1,则中间四边形E1F1G1H1的面积等于查看答案和解析>>
科目:初中数学 来源: 题型:
A、m<
| ||
B、m≤
| ||
C、m<
| ||
D、m≤
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com