
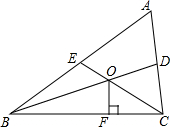
 如图,△ABC的中线BD、CE相交于点O,OF⊥BC,且AB=7,BC=6,AC=4,OF=2,则四边形ADOE的面积是6.
如图,△ABC的中线BD、CE相交于点O,OF⊥BC,且AB=7,BC=6,AC=4,OF=2,则四边形ADOE的面积是6. 分析 首先根据三角形的面积=底×高÷2,求出△BOC的面积是多少;然后根据三角形的中线将三角形分成面积相等的两部分,可得△BCD、△ACE的面积均是△ABC的面积的一半,据此判断出四边形ADOE的面积等于△BOC的面积,据此解答即可.
解答 解:∵BD、CE均是△ABC的中线,
∴S△BCD=S△ACE=$\frac{1}{2}$S△ABC,
∴S四边形ADOE+S△COD=S△BOC+S△COD,
∴S四边形ADOE=S△BOC=6×2÷2=6.
故答案为:6.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的性质,要熟练掌握,解答此题的关键要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)三角形的面积=底×高÷2.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{m+n}{25}$ | B. | $\frac{25m+20n}{45}$ | C. | $\frac{m+n}{2}$ | D. | $\frac{20(m+n)}{45}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
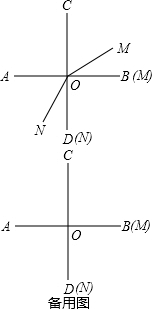 如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角)
如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
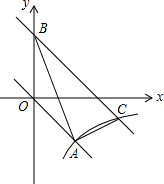 如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com