
 如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可).
如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可). 分析 添加条件OD=OE,再由条件CO平分∠∠AOE,可得∠BOC=∠AOC,再根据SAS定理判定两个三角形全等即可.
解答 解:添加条件OD=OE,
∵CO平分∠∠AOE,
∴∠BOC=∠AOC,
在△EOP和△DOP中,
$\left\{\begin{array}{l}{EO=DO}\\{∠EOP=∠DOP}\\{OP=OP}\end{array}\right.$,
∴△EOP≌△DOP(SAS).
故答案为:OD=OE.
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2(x+2)2+1 | B. | y=2(x-2)2+1 | C. | y=2(x+2)2-1 | D. | y=2(x-2)2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
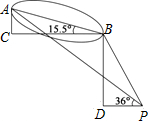 有“小蛮腰”之称的广州电视塔为中国第一高电视塔,其主体顶部450~454米处有世界最高摩天轮(即图中AC=4米),与一般竖立的摩天轮不一样,广州塔的摩天轮沿着倾斜的轨道运转,对地倾斜角为∠ABC=15.5°.小明操作无人机观察摩天轮,由于设备限制无法近距离拍摄,无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°,最高点A的仰角为∠APD=36°,请问此时无人机距离电视塔的水平距离PD为( )(参考数据:tan15.5°≈0.4,tan36°≈0.7,$\sqrt{3}$≈1.7)
有“小蛮腰”之称的广州电视塔为中国第一高电视塔,其主体顶部450~454米处有世界最高摩天轮(即图中AC=4米),与一般竖立的摩天轮不一样,广州塔的摩天轮沿着倾斜的轨道运转,对地倾斜角为∠ABC=15.5°.小明操作无人机观察摩天轮,由于设备限制无法近距离拍摄,无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°,最高点A的仰角为∠APD=36°,请问此时无人机距离电视塔的水平距离PD为( )(参考数据:tan15.5°≈0.4,tan36°≈0.7,$\sqrt{3}$≈1.7)| A. | 3 | B. | 2.7 | C. | 3.3 | D. | 3.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一个边长为1的正方形纸片分割成6部分,部分①是整体面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成6部分,部分①是整体面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
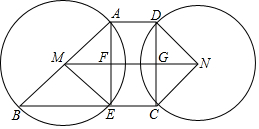 如图,已知四边形BCNM是平行四边形,分别以M,N为圆心,以MB,NC为半径作圆,⊙M交BC于E,AB为⊙M的直径,连接AE交MN于F,过C点作MN的垂线MN于G,交⊙N于D,连接DN.
如图,已知四边形BCNM是平行四边形,分别以M,N为圆心,以MB,NC为半径作圆,⊙M交BC于E,AB为⊙M的直径,连接AE交MN于F,过C点作MN的垂线MN于G,交⊙N于D,连接DN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com