

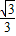 AD=
AD= ,OA=2OD=
,OA=2OD= ,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积.
,然后利用AB与⊙O所形成的弓形的面积=S扇形OAB-S△OAB,最后把两个结果相加即可得到两圆公共部分的面积. 解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB.
解:如图,连OO′交AB于D,交⊙O于C,则OO′垂直平分AB. -
- ×22=
×22= π-
π- ;
; AD=
AD= ,
, ,
, -
- ×2×
×2× =
= π-
π- ,
, π-
π- +
+ π-
π- =
= π-
π- .
. π-
π- .
. ;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系.
;也考查了相交两圆的性质、等边三角形的性质以及含30度的直角三角形三边的关系. 

科目:初中数学 来源: 题型:
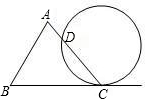 如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 |
| CD |
| A、50° | B、60° |
| C、100° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数![]() 和反比例函数
和反比例函数![]() 的图像交于A、B两点.
的图像交于A、B两点.
(1)利用图中条件,求出两个函数的解析式;
(2)根据图像写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》好题集(07):5.5 直线与圆的位置关系(解析版) 题型:选择题
 的度数为何( )
的度数为何( )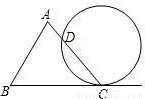
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com