练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ⊙O的直径为10，圆心O到弦AB的距离为3，则弦AB的长是________．

    8
    分析：先求出半径，再利用勾股定理求出半弦长，弦长就可以求出了．
    解答：解：如图，根据题意，得
    OA=×10=5，AE===4
    ∴AB=2AE=8．
    点评：利用半径、半弦长、弦心距构造直角三角形，利用勾股定理求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：如图，⊙O的直径为10，弦AC=8，点B在圆周上运动（与A、C两点不重合），连接BC、BA，过点C作CD⊥AB于D、设CB的长为x，CD的长为y．
    （1）求y关于x的函数关系式；当以BC为直径的圆与AC相切时，求y的值；
    （2）在点B运动的过程中，以CD为直径的圆与⊙O有几种位置关系，并求出不同位置时y的取值范围；
    （3）在点B运动的过程中，如果过B作BE⊥AC于E，那么以BE为直径的圆与⊙O能内切吗？若不能，说明理由；若能，求出BE的长．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、电脑CPU蕊片由一种叫“单晶硅”的材料制成，未切割前的单晶硅材料是一种薄型圆片，叫“晶圆片”．现为了生产某种CPU蕊片，需要长、宽都是1cm的正方形小硅片若干．如果晶圆片的直径为10.05cm．问一张这种晶圆片能否切割出所需尺寸的小硅片66张？请说明你的方法和理由．（不计切割损耗）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•长宁区一模）已知圆⊙O的直径为10，弦AB的长度为8，M是弦AB上一动点，设线段OM=d，则d的取值范围是
    3≤d≤5
    3≤d≤5
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

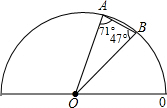    （2012•南昌模拟）一量角器所在圆的直径为10厘米，其外缘有A、B两点，其读数、分别为71°和47°．
    （1）劣弧AB所对圆心角是多少度？
    （2）求劣弧AB的长；
    （3）问A、B之间的距离是多少？（可用计算器，精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一点到圆周上点的最大距离为9，最短距离为1，则圆的直径为
    10或8
    10或8
    ．

    查看答案和解析>>

    同步练习册答案