
【题目】已知:如图,△ABC中,AB=4,AC=6,AD平分∠BAC,且BD⊥AD于D,交AC于F,E是BC的中点,连接DE.求:DE的长度. 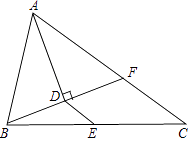
 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).

(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
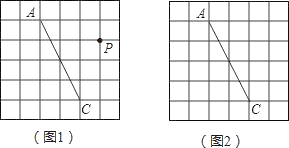
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com