
��ͼ��ֱ�� ��
�� ���
��� ��ֱ��ཻ��A��B���㣬ƽ����ֱ��
��ֱ��ཻ��A��B���㣬ƽ����ֱ�� ��ֱ��
��ֱ�� ��ԭ��O��������
��ԭ��O�������� �����������ÿ��1����λ���ȵ��ٶ��˶�������
�����������ÿ��1����λ���ȵ��ٶ��˶�������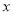 ���
��� ��ֱ��ཻ��C��D���㣬�˶�ʱ��Ϊ
��ֱ��ཻ��C��D���㣬�˶�ʱ��Ϊ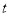 �루
�루 ������CDΪб��������ֱ�ǡ�CDE��E��O����ֱ���CD���ࣩ������CDE�͡�OAB���غϲ��ֵ����Ϊ
������CDΪб��������ֱ�ǡ�CDE��E��O����ֱ���CD���ࣩ������CDE�͡�OAB���غϲ��ֵ����Ϊ ����
���� ��
�� ֮��ĺ�����ϵ��ͼ������ǣ� ��
֮��ĺ�����ϵ��ͼ������ǣ� ��

A. A B. B C. C D. D
C ���������������: ��ʱ, �� ʱ, �۲�ͼ���֪��S��t֮��ĺ�����ϵ��ͼ�������C. �ʴ�ΪC.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
��ͼ����ABC����������ֱ�������������ĸ���ϣ���tanC��ֵ�ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
�ֽ���ʽ��x2y-4xy+4y=___________
y(x-2)2 �����������������x2y-4xy+4y=y��x2-4x+4��=y(x-2)2. �ʴ�Ϊ��y(x-2)2.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
������ABCD�ı߳�Ϊ3��E��F�ֱ���AB��BC���ϵĵ㣬�ҡ�EDF��45�㣬����DAE�Ƶ�D��ʱ����ת90�㣬�õ���DCM.

(1)��֤��EF��FM��
(2)��AE��1ʱ����EF�ij���
��1�������������2��. �������������������1������ת�����ʿ�֪��DE=DM����EDM=90�㣬��Ϊ��EDF=45�㣬���ԡ�FDM=��EDM=45�㣬ͨ��֤����DEF�ա�DMF�õ�EF=MF�� ��2����EF=MF=x����BF=4-x��BE=2����Rt��EBF�У��ɹ��ɶ����õ�����x�ĵ�ʽ�����x��ֵ���ɣ� �����������1��֤�����ߡ�DAE��ʱ����ת90��õ���DCM�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AB=5��BC=3��AC=4���Ե�CΪԲ�ĵ�Բ��AB���У����C�İ뾶Ϊ____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
��֪һԪ���η��� ��һ����Ϊ2������һ��Ϊ��������
��һ����Ϊ2������һ��Ϊ��������
A. -4 B. -2 C. 4 D. 2
D ���������������: �����x��һԪ���η��̵���һ����Ϊt���� ���t=2. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
��֪����ͼ���ڡ�ABC�У�AB=AC��AD��BC������Ϊ��D��AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E��
��1����֤���ı���ADCEΪ���Σ�
��2������ABC����ʲô����ʱ���ı���ADCE��һ�������Σ�������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
˳�����������ı����ı��е����õ��ı���һ���ǣ� ��
A��ƽ���ı��� B������ C������ D��������
A �������� ���������˳�����������ı����ı��е����õ��ı��Σ�һ��Ա�ƽ�в��ҵ���ԭ���ı���ijһ�Խ��ߵ�һ�룬˵�����ı��εĶԱ�ƽ������ȣ�������ƽ���ı��Σ� �������� ����BD�� ��֪�����ı���ABCD��E��F��G��H�ֱ��Ǹ����е㣮 ���ڡ�ABD�У�E��H��AB��AD�е㣬 ��EH��BD��EH=BD�� ���ڡ�BCD�У�G��F��DC��BC�е㣬 ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ݸ�к���ѧУ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ���word�溬�𰸽����� ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У���P����1��2����λ���ڣ� ��
A.��һ���� B.�ڶ����� C.�������� D.��������
B �������� ���������������Ҫ������ƽ��ֱ������ϵ�и������ĵ������ķ����ص㣮�ĸ����ķ����ص�ֱ��ǣ���һ���ޣ�+��+�����ڶ����ޣ�����+�����������ޣ������������������ޣ�+���������ߵ�P����1��2���ĺ����ꩁ1��0��������2��0�����P�ڵڶ����ޣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com