
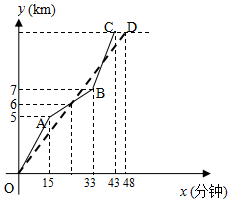
 如图表示两名选手在一次自行车越野赛中,路程y(km)随时间x(分)变化的图象(全程),根据图象回答以下问题:
如图表示两名选手在一次自行车越野赛中,路程y(km)随时间x(分)变化的图象(全程),根据图象回答以下问题:分析 (1)根据点A、B的坐标利用待定系数法求出线段AB的解析式,再代入y=6求出x值即可得出结论;
(2)由第一次相遇的时间可得出线段AB、OD的交点坐标,利用待定系数法可求出线段OD的解析式,再代入x=48求出y值即可得出结论;
(3)根据点B、C的坐标利用待定系数法求出线段BC的解析式,联立线段BC、OD的解析式成方程组,即可求出两人第二次相遇的时间;
(4)设在两次相遇之间,两人之间的距离为s,结合图形可得出当24≤x≤33和33≤x≤38时,s关于x的函数解析式,再利用一次函数的性质即可解决最值问题.
解答 解:(1)设线段AB的解析式为y=ax+b,
将点A(15,5)、B(33,7)代入y=ax+b,
$\left\{\begin{array}{l}{15a+b=5}\\{33a+b=7}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{1}{9}}\\{b=\frac{10}{3}}\end{array}\right.$,
∴线段AB的解析式为y=$\frac{1}{9}$x+$\frac{10}{3}$(15≤x≤33).
当y=$\frac{1}{9}$x+$\frac{10}{3}$=6时,x=24.
答:比赛开始24分钟时,两人第一次相遇.
(2)设线段OD的解析式为y=kx,
将(24,6)代入y=kx,
6=24k,解得:k=$\frac{1}{4}$,
∴线段OD的解析式为y=$\frac{1}{4}$x(0≤x≤48).
当x=48时,y=$\frac{1}{4}$x=12.
答:这次比赛全程是12千米.
(3)设线段BC的解析式为y=mx+n,
将B(33,7)、C(43,12)代入y=mx+n,
$\left\{\begin{array}{l}{33m+n=7}\\{43m+n=12}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=-\frac{19}{2}}\end{array}\right.$,
∴线段BC的解析式为y=$\frac{1}{2}$x-$\frac{19}{2}$(33≤x≤43).
联立线段BC、OD的解析式成方程组,
$\left\{\begin{array}{l}{y=\frac{1}{2}x-\frac{19}{2}}\\{y=\frac{1}{4}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=38}\\{y=\frac{19}{2}}\end{array}\right.$.
答:比赛开始38分钟时,两人第二次相遇.
(4)设在两次相遇之间,两人之间的距离为s,
当24≤x≤33时,s=$\frac{1}{4}$x-($\frac{1}{9}$x+$\frac{10}{3}$)=$\frac{5}{36}$x-$\frac{10}{3}$,
∵$\frac{5}{36}$>0,
∴当x=33时,s取最大值,最大值为$\frac{5}{4}$;
当33≤x≤38时,s=$\frac{1}{4}$x-($\frac{1}{2}$x-$\frac{19}{2}$)=-$\frac{1}{4}$x+$\frac{19}{2}$,
∵-$\frac{1}{4}$<0,
∴当x=33时,s取最大值,最大值为$\frac{5}{4}$.
答:在两次相遇之间,两人相距最远的距离是$\frac{5}{4}$千米.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点A、B的坐标利用待定系数法求出线段AB的解析式;(2)根据第一次相遇时点的坐标利用待定系数法可求出线段OD的解析式;(3)根据点B、C的坐标利用待定系数法求出线段BC的解析式;(4)分24≤x≤33和33≤x≤38,找出s关于x的函数解析式.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.
如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
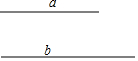 画图:已知线段a、b(不要求写画法,但要写出结论).
画图:已知线段a、b(不要求写画法,但要写出结论).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
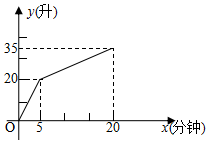 有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?
有一个附有进、出水管的容器,每单位时间进、出水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水也出水,便得到x(分钟)与水量y(升)之间的关系如图.若20分钟后只放水不进水,则第( )分钟可将容器中的水放完?| A. | $\frac{95}{4}$ | B. | $\frac{95}{3}$ | C. | $\frac{95}{2}$ | D. | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果增加条件AC=A′C′,那么△ABC≌△A′B′C′(SAS) | |
| B. | 如果增加条件BC=B′C′,那么△ABC≌△A′B′C′(SAS) | |
| C. | 如果增加条件∠B=∠B′,那么△ABC≌△A′B′C′(ASA) | |
| D. | 如果增加条件∠C=∠C′,那么△ABC≌△A′B′C′(AAS) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com