
分析 (1)根据表达式是整式,自变量取全体实数解答;
(2)根据分母不等于0列不等式求解即可;
(3)根据被开方数大于等于0列不等式求解即可;
(4)根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:(1)x取全体实数;
(2)由题意得,4-x≠0,
解得x≠4;
(3)由题意得,x-2≥0且3-x≥0,
解得x≥2且x≤3,
所以,2≤x≤3;
(4)由题意得,x+2≥0且$\sqrt{x+2}$-2≠0,
解得x≥-2且x≠2.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
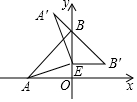 如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.
如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3,使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为$\frac{32\sqrt{3}}{27}$.
如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3,使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为$\frac{32\sqrt{3}}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
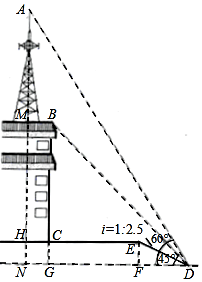 如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com