
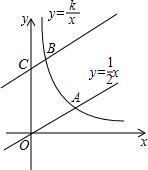
 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.分析 (1)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设A(3x,$\frac{3}{2}$x),由于OA=3BC,故可得出B(x,$\frac{1}{2}$x+4),再根据反比例函数中k=xy为定值求出k的值即可;
(2)由(1)得出点A、B的坐标后,利用割补法求解可得.
解答 解:(1)分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,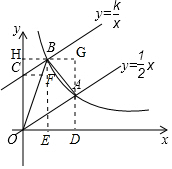
设A(3x,$\frac{3}{2}$x),
∵OA=3BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=$\frac{1}{3}$OD,
∵点B在直线y=$\frac{1}{2}$x+4上,
∴B(x,$\frac{1}{2}$x+4),
∵点A、B在双曲线y=$\frac{k}{x}$上,
∴3x•$\frac{3}{2}$x=x•($\frac{1}{2}$x+4),解得x=1,
∴k=3×1×$\frac{3}{2}$×1=$\frac{9}{2}$;
(2)由(1)知点A(3,$\frac{3}{2}$)、B(1,$\frac{9}{2}$),
则S△AOB=S矩形ODGH-S△AOD-S△BOH-S△ABG
=3×$\frac{9}{2}$-$\frac{9}{4}$-$\frac{9}{4}$-$\frac{1}{2}$×2×3
=6.
点评 本题考查的是反比例函数与一次函数的交点问题,根据题意作出辅助线,设出A、B两点的坐标,再根据k=xy的特点求出k的值即可.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:填空题
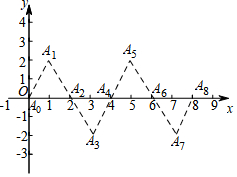 如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).
如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 电器类型 | 进价(元)/台 | 售价(元)/台 |
| 甲 | 1500 | 1900 |
| 乙 | 1800 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
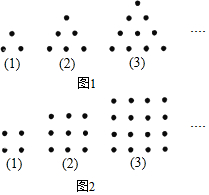 古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.
古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
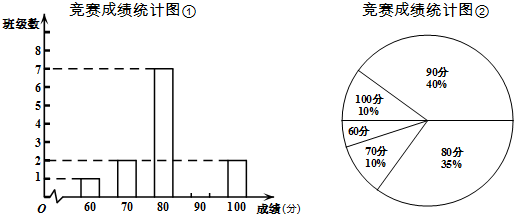
| A. | 这次竞赛各班平均成绩是84 | |
| B. | 这次各班成绩组成的一组数据中的中位数是85 | |
| C. | 这次各班成绩组成的一组数据中的极差是40 | |
| D. | 这次各班成绩组成的一组数据中的众数是80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com