
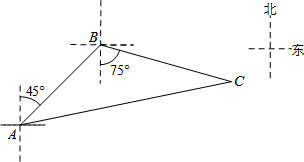
 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 分析 设巡逻船从出发到成功拦截所用时间为x小时,由题意得出∠ABC=120°,AB=12,BC=10x,AC=14x,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,由三角函数得出BD、AD的长度,得出CD=10x+6.在Rt△ACD中,由勾股定理得出方程,解方程即可.
解答 解: 设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°-75°)=60°,
∴BD=AB•cos60°=$\frac{1}{2}$AB=6,AD=AB•sin60°=6$\sqrt{3}$,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得:${({14x})^2}={({10x+6})^2}+{({6\sqrt{3}})^2}$,
解得:${x_1}=2,{x_2}=-\frac{3}{4}$(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时.
点评 本题考查了解直角三角形的应用、勾股定理、三角函数;由三角函数和勾股定理得出方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
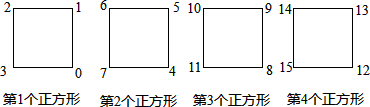
| A. | 第504个正方形的左下角 | B. | 第504个正方形的右下角 | ||
| C. | 第505个正方形的左上角 | D. | 第505个正方形的右下角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
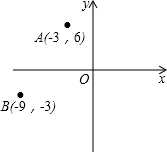 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com